Extrémy funkce. Extrém funkce Zvyšující a klesající funkce
S touto službou můžete najít největší a nejmenší hodnotu funkce jedna proměnná f(x) s řešením naformátovaným ve Wordu. Je-li tedy dána funkce f(x,y), je nutné najít extrém funkce dvou proměnných. Můžete také najít intervaly rostoucích a klesajících funkcí.
Pravidla pro zadávání funkcí:
Nutná podmínka pro extrém funkce jedné proměnné
Rovnice f" 0 (x *) = 0 je nezbytnou podmínkou pro extrém funkce jedné proměnné, tj. v bodě x * musí první derivace funkce zaniknout. Identifikuje stacionární body x c, ve kterých funkce nezaniká. zvýšit nebo snížit.Dostatečná podmínka pro extrém funkce jedné proměnné
Nechť f 0 (x) je dvakrát diferencovatelné vzhledem k x patřícímu do množiny D. Pokud je v bodě x * splněna podmínka:F" 0 (x *) = 0
f"" 0 (x *) > 0
Potom bod x * je lokální (globální) minimální bod funkce.
Pokud je v bodě x * splněna podmínka:
F" 0 (x *) = 0
f"" 0 (x *)< 0
Potom bod x * je lokální (globální) maximum.
Příklad č. 1. Najděte největší a nejmenší hodnoty funkce: na segmentu.
Řešení. ![]()
Kritický bod je jedna x 1 = 2 (f’(x)=0). Tento bod patří do segmentu. (Bod x=0 není kritický, protože 0∉).
Vypočítáme hodnoty funkce na koncích segmentu a v kritickém bodě.
f(1)=9, f(2)= 5/2, f(3)=3 8/81
Odpověď: f min = 5 / 2 při x = 2; f max = 9 při x = 1
Příklad č. 2. Pomocí derivací vyšších řádů najděte extrém funkce y=x-2sin(x) .
Řešení.
Najděte derivaci funkce: y’=1-2cos(x) . Najděte kritické body: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. Najdeme y’’=2sin(x), vypočítejte , což znamená x= π / 3 +2πk, k∈Z jsou minimální body funkce; ![]() , což znamená x=- π / 3 +2πk, k∈Z jsou maximální body funkce.
, což znamená x=- π / 3 +2πk, k∈Z jsou maximální body funkce.
Příklad č. 3. Vyšetřte extrémní funkci v okolí bodu x=0.
Řešení. Zde je potřeba najít extrémy funkce. Pokud je extrém x=0, zjistěte jeho typ (minimum nebo maximum). Pokud mezi nalezenými body není x = 0, pak vypočítejte hodnotu funkce f(x=0).
Je třeba si uvědomit, že když derivace na každé straně daného bodu nemění své znaménko, nejsou možné situace vyčerpány ani pro diferencovatelné funkce: může se stát, že pro libovolně malé okolí na jedné straně bodu x 0 resp. na obou stranách derivace mění znaménko. V těchto bodech je nutné použít jiné metody ke studiu funkcí v extrému.
Příklad č. 4. Rozdělte číslo 49 na dva členy, jejichž součin bude největší.
Řešení. Označme x jako první člen. Potom (49-x) je druhý člen.
Produkt bude maximálně: x·(49-x) → max
nebo
49x - x 2
Největší objem válce
Najděte rozměry válce s největším objemem vyrobeného z obrobku ve tvaru koule o poloměru R.Řešení:

Objem válce je: V = πr 2 H
kde H = 2 h,
Dosaďte tyto hodnoty do účelové funkce.
V → max
Pojďme najít extrém funkce. Protože objemová funkce V(h) závisí pouze na jedné proměnné, najdeme derivaci pomocí služby
Z tohoto článku se čtenář dozví o tom, co je extrém funkční hodnoty, a také o vlastnostech jeho použití v praktických činnostech. Studium takového konceptu je nesmírně důležité pro pochopení základů vyšší matematiky. Toto téma je zásadní pro hlubší studium předmětu.
V kontaktu s
Co je to extrém?
Ve školním kurzu je uvedeno mnoho definic pojmu „extrém“. Tento článek má poskytnout nejhlubší a nejjasnější pochopení termínu pro ty, kteří tuto problematiku neznali. Pod pojmem se tedy rozumí, do jaké míry nabývá funkční interval minimální nebo maximální hodnoty na konkrétní množině.
Extrém je zároveň minimální a zároveň maximální hodnotou funkce. Existuje minimální bod a maximální bod, to znamená extrémní hodnoty argumentu v grafu. Hlavní vědy, které používají tento koncept, jsou:
- statistika;
- ovládání stroje;
- ekonometrie.
Extrémní body hrají důležitou roli při určování posloupnosti dané funkce. Souřadnicový systém v grafu nejlépe ukazuje změnu krajní polohy v závislosti na změně funkčnosti.
Extrémy derivační funkce
Existuje také fenomén jako „derivát“. Je nutné určit extrémní bod. Je důležité nezaměňovat minimální nebo maximální body s nejvyšší a nejnižší hodnotou. Jsou to různé pojmy, i když se mohou zdát podobné.
Hodnota funkce je hlavním faktorem při určování způsobu nalezení maximálního bodu. Derivát není tvořen z hodnot, ale výhradně z jeho krajní polohy v tom či onom řádu.
Samotná derivace je určena na základě těchto extrémních bodů, nikoli na základě největší nebo nejmenší hodnoty. V ruských školách není hranice mezi těmito dvěma pojmy jasně nakreslena, což ovlivňuje chápání tohoto tématu obecně.
Podívejme se nyní na takový pojem jako „akutní extrém“. Dnes existuje akutní minimální hodnota a akutní maximální hodnota. Definice je uvedena v souladu s ruskou klasifikací kritických bodů funkce. Koncept extrémního bodu je základem pro nalezení kritických bodů v grafu.

K definování takového konceptu se uchýlí k použití Fermatova teorému. Je to nejdůležitější při studiu extrémních bodů a dává jasnou představu o jejich existenci v té či oné podobě. Pro zajištění extrémnosti je důležité vytvořit na grafu určité podmínky pro pokles nebo nárůst.
Chcete-li přesně odpovědět na otázku „jak najít maximální bod“, musíte dodržovat následující pokyny:
- Nalezení přesné domény definice v grafu.
- Hledání derivace funkce a extremního bodu.
- Vyřešte standardní nerovnice pro doménu, kde je argument nalezen.
- Umět dokázat, ve kterých funkcích je bod na grafu definovaný a spojitý.

Pozornost! Hledání kritického bodu funkce je možné pouze v případě, že existuje derivace alespoň druhého řádu, což je zajištěno vysokým podílem přítomnosti extrémního bodu.
Nezbytná podmínka pro extrém funkce
Aby existoval extrém, je důležité, aby existoval minimální i maximální počet bodů. Pokud je toto pravidlo dodrženo jen částečně, pak je porušena podmínka existence extrému.

Každá funkce na jakékoli pozici musí být odlišena, aby bylo možné identifikovat její nové významy. Je důležité pochopit, že případ bodu klesajícího k nule není hlavním principem pro nalezení diferencovatelného bodu.
Akutní extrém, stejně jako minimum funkce, je nesmírně důležitým aspektem řešení matematického problému pomocí extrémních hodnot. Pro lepší pochopení této komponenty je důležité použít tabulkové hodnoty pro specifikaci funkčnosti.
| Výzkum plného významu | Vykreslení grafu hodnot |
| 1. Určení bodů rostoucích a klesajících hodnot. 2. Hledání bodů nespojitosti, extrému a průsečíku se souřadnicovými osami. 3. Proces určování změn polohy na grafu. 4. Určení ukazatele a směru konvexity a konvexity s přihlédnutím k přítomnosti asymptot. 5. Tvorba souhrnné tabulky výzkumu z pohledu určení jejích souřadnic. 6. Hledání intervalů rostoucích a klesajících krajních a ostrých bodů. 7. Stanovení konvexnosti a konkávnosti křivky. 8. Vynesení grafu s přihlédnutím k výzkumu vám umožní najít minimum nebo maximum. |
Hlavním prvkem při práci s extrémy je přesná konstrukce jeho grafu. Učitelé školy tak důležitému aspektu, který je hrubým porušením výchovně vzdělávacího procesu, často nevěnují maximální pozornost. Ke konstrukci grafu dochází pouze na základě výsledků studia funkčních dat, identifikace akutních extrémů a také bodů na grafu. Ostré extrémy derivační funkce jsou zobrazeny na grafu přesných hodnot standardním postupem pro stanovení asymptot. Maximální a minimální body funkce jsou doprovázeny složitějšími konstrukcemi grafů. To je způsobeno hlubší potřebou propracovat se s problémem akutního extrému. Je také nutné najít derivaci komplexní a jednoduché funkce, protože to je jeden z nejdůležitějších konceptů v problému extrému. |
Extrém funkčního
Chcete-li zjistit výše uvedenou hodnotu, musíte dodržovat následující pravidla:
- určit nezbytnou podmínku pro extrémní vztah;
- vzít v úvahu dostatečný stav krajních bodů na grafu;
- provést výpočet akutního extrému.
Používají se také pojmy jako slabé minimum a silné minimum. To je třeba vzít v úvahu při stanovení extrému a jeho přesném výpočtu. Akutní funkcionalita je přitom vyhledání a vytvoření všech nezbytných podmínek pro práci s grafem funkce.
Jedná se o poměrně zajímavý úsek matematiky, se kterým se setkávají naprosto všichni absolventi a studenti. Ne každému se však matan líbí. Někteří nedokážou pochopit ani základní věci, jako je zdánlivě standardní funkční studie. Tento článek je určen k nápravě takového nedopatření. Chcete se dozvědět více o funkční analýze? Chtěli byste vědět, co jsou extrémní body a jak je najít? Pak je tento článek právě pro vás.
Studium grafu funkce
Za prvé, stojí za to pochopit, proč je vůbec nutné analyzovat graf. Existují jednoduché funkce, které není těžké nakreslit. Pozoruhodným příkladem takové funkce je parabola. Nakreslit graf nebude těžké. Stačí pomocí jednoduché transformace najít čísla, ve kterých funkce nabývá hodnoty 0. A to je v zásadě vše, co potřebujete vědět, abyste mohli nakreslit graf paraboly.
Ale co když je funkce, kterou potřebujeme vykreslit, mnohem složitější? Protože vlastnosti komplexních funkcí nejsou zcela zřejmé, je nutné provést celkovou analýzu. Teprve poté lze funkci znázornit graficky. Jak to udělat? Odpověď na tuto otázku najdete v tomto článku.
Plán funkční analýzy
První věc, kterou musíme udělat, je provést povrchní studii funkce, během níž najdeme doménu definice. Začněme tedy popořadě. Definiční doména je množina hodnot, kterými je funkce definována. Jednoduše řečeno, jde o čísla, která lze použít ve funkci místo x. Pro určení rozsahu se stačí podívat do záznamu. Například je zřejmé, že funkce y (x) = x 3 + x 2 - x + 43 má definiční obor, kterým je množina reálných čísel. No, s funkcí jako (x 2 - 2x)/x je všechno trochu jinak. Protože číslo ve jmenovateli se nesmí rovnat 0, definičním oborem této funkce budou všechna reálná čísla jiná než nula.
Dále je potřeba najít tzv. nuly funkce. Toto jsou hodnoty argumentů, při kterých má celá funkce hodnotu nula. K tomu je nutné funkci přirovnat k nule, podrobně ji zvážit a provést některé transformace. Vezměme si nám již známou funkci y(x) = (x 2 - 2x)/x. Ze školního kurzu víme, že zlomek je roven 0, když je čitatel roven nule. Proto zahodíme jmenovatele a začneme pracovat s čitatelem a přirovnáme jej k nule. Dostaneme x 2 - 2x = 0 a vyjmeme x ze závorek. Proto x (x - 2) = 0. Ve výsledku zjistíme, že naše funkce je rovna nule, když se x rovná 0 nebo 2.
Při studiu grafu funkce se mnoho lidí setkává s problémy v podobě extrémních bodů. A je to zvláštní. Koneckonců, extrémy jsou docela jednoduché téma. Nevěříš mi? Přesvědčte se sami přečtením této části článku, ve které budeme hovořit o minimálních a maximálních bodech.

Za prvé, stojí za to pochopit, co je extrém. Extrém je mezní hodnota, které funkce dosáhne v grafu. Ukazuje se, že existují dvě extrémní hodnoty - maximální a minimální. Pro názornost se můžete podívat na obrázek výše. Ve studované oblasti je bod -1 maximem funkce y (x) = x 5 - 5x a bod 1 je tedy minimem.
Nepleťte si také pojmy. Extrémní body funkce jsou ty argumenty, ve kterých daná funkce nabývá extrémních hodnot. Na druhé straně, extrém je hodnota minima a maxima funkce. Zvažte například znovu obrázek výše. -1 a 1 jsou extrémní body funkce a 4 a -4 jsou samotné extrémy.
Hledání extrémních bodů

Ale jak najdete extrémní body funkce? Všechno je docela jednoduché. První věc, kterou musíte udělat, je najít derivaci rovnice. Řekněme, že jsme dostali úkol: „Najděte extrémní body funkce y (x), x je argument Pro názornost vezměme funkci y (x) = x 3 + 2x 2 + x + 54. Derivujme a. dostaneme následující rovnici: 3x 2 + 4x + 1. Výsledkem je standardní kvadratická rovnice. Dále je třeba ji přirovnat k nule a najít kořeny, protože diskriminant je větší než nula (D = 16 - 12 = 4), tato rovnice je určena dvěma kořeny a získáme je: 1/3 a -1 je kdo Který bod je maximum a který minimum Chcete-li to provést, musíte vzít sousední bod a zjistit jeho hodnotu, vzít číslo -2, které je umístěno vlevo podél souřadnicové čáry od -. 1. Dosadíme tuto hodnotu do naší rovnice y(-2) = 12 - 8 + 1 = 5. Výsledkem je kladné číslo To znamená, že v intervalu od 1/3 do -1. To zase znamená, že na intervalech od mínus nekonečna do 1/3 a od -1 do plus nekonečna funkce klesá. Můžeme tedy uzavřít, že číslo 1/3 je minimální bod funkce na studovaném intervalu a -1 je maximální bod.

Za zmínku také stojí, že jednotná státní zkouška vyžaduje nejen nalezení extrémních bodů, ale také provedení nějaké operace s nimi (sčítání, násobení atd.). Z tohoto důvodu stojí za to věnovat zvláštní pozornost podmínkám problému. Nepozorností totiž můžete přijít o body.
Extrémní bod funkce je bod v oboru definice funkce, ve kterém hodnota funkce nabývá minimální nebo maximální hodnoty. Hodnoty funkce v těchto bodech se nazývají extrémy (minimum a maximum) funkce.
Definice. Tečka X1 funkční doména F(X) je nazýván maximální bod funkce , pokud je hodnota funkce v tomto bodě větší než hodnoty funkce v bodech dostatečně blízko k ní, umístěných napravo a nalevo od ní (to znamená, že nerovnost platí F(X0 ) > F(X 0 + Δ X) X1 maximum.
Definice. Tečka X2 funkční doména F(X) je nazýván minimální bod funkce, pokud je hodnota funkce v tomto bodě menší než hodnoty funkce v bodech dostatečně blízko k ní, umístěných napravo a nalevo od ní (to znamená, že nerovnost platí F(X0 ) < F(X 0 + Δ X) ). V tomto případě říkáme, že funkce má v bodě X2 minimální.
Řekněme bod X1 - maximální bod funkce F(X). Poté v intervalu až X1 funkce se zvyšuje, takže derivace funkce je větší než nula ( F "(X) > 0 ) a v intervalu po X1 funkce se tedy snižuje, derivace funkce méně než nula ( F "(X) < 0 ). Тогда в точке X1
Předpokládejme také, že bod X2 - minimální bod funkce F(X). Poté v intervalu až X2 funkce je klesající a derivace funkce je menší než nula ( F "(X) < 0 ), а в интервале после X2 funkce je rostoucí a derivace funkce je větší než nula ( F "(X) > 0). V tomto případě také na místě X2 derivace funkce je nulová nebo neexistuje.
Fermatova věta (nezbytný znak existence extrému funkce). Pokud bod X0 - extrémní bod funkce F(X), pak v tomto bodě je derivace funkce rovna nule ( F "(X) = 0 ) nebo neexistuje.
Definice. Volají se body, ve kterých je derivace funkce nulová nebo neexistuje kritické body .

Příklad 1. Zvažme funkci.
Na místě X= 0 derivace funkce je nulová, tedy bod X= 0 je kritický bod. Jak je však vidět na grafu funkce, zvyšuje se v celém definičním oboru, tedy bod X= 0 není krajní bod této funkce.
Tedy podmínky, že derivace funkce v bodě je rovna nule nebo neexistuje, jsou pro extrém nezbytnými podmínkami, ale ne postačujícími, protože lze uvést další příklady funkcí, pro které jsou tyto podmínky splněny, ale funkce nemá v odpovídajícím bodě extrém. Proto musí existovat dostatek důkazů, což umožňuje posoudit, zda existuje extrém v konkrétním kritickém bodě a jaký druh extrému to je - maximální nebo minimální.
Věta (první dostatečný znak existence extrému funkce). Kritický bod X0 F(X) jestliže při průchodu tímto bodem derivace funkce změní znaménko a změní-li se znaménko z „plus“ na „mínus“, pak jde o maximální bod, a pokud z „mínus“ na „plus“, pak je to minimální bod.
Pokud je blízko bodu X0 , nalevo a napravo od něj si derivace zachovává znaménko, to znamená, že funkce buď pouze klesá, nebo jen roste v nějakém okolí bodu X0 . V tomto případě v bodě X0 neexistuje žádný extrém.
Tak, Chcete-li určit extrémní body funkce, musíte provést následující :
- Najděte derivaci funkce.
- Přirovnejte derivaci k nule a určete kritické body.
- V duchu nebo na papíře označte kritické body na číselné ose a určete znaménka derivace funkce ve výsledných intervalech. Pokud se znaménko derivace změní z „plus“ na „mínus“, pak je kritickým bodem maximální bod a pokud z „mínus“ na „plus“, pak minimální bod.
- Vypočítejte hodnotu funkce v extrémních bodech.

Příklad 2 Najděte extrémy funkce ![]() .
.
Řešení. Pojďme najít derivaci funkce:
Přirovnejme derivaci k nule, abychom našli kritické body:
![]() .
.
Protože pro žádné hodnoty „x“ není jmenovatel roven nule, srovnáme čitatele s nulou:
Mám jeden kritický bod X= 3. Určeme znaménko derivace v intervalech ohraničených tímto bodem:
v rozsahu od mínus nekonečna do 3 - znaménko mínus, to znamená, že funkce klesá,
v intervalu od 3 do plus nekonečna je znaménko plus, to znamená, že funkce roste.
Tedy tečka X= 3 je minimální bod.
Pojďme najít hodnotu funkce v minimálním bodě:
Je tedy nalezen extrémní bod funkce: (3; 0) a je to minimální bod.
Věta (druhý dostatečný znak existence extrému funkce). Kritický bod X0 je krajní bod funkce F(X) pokud druhá derivace funkce v tomto bodě není rovna nule ( F ""(X) ≠ 0 ), a pokud je druhá derivace větší než nula ( F ""(X) > 0 ), pak maximální bod, a pokud je druhá derivace menší než nula ( F ""(X) < 0 ), то точкой минимума.
Poznámka 1. Pokud v bodě X0 Pokud zmizí jak první, tak i druhá derivace, pak v tuto chvíli není možné posuzovat přítomnost extrému na základě druhého dostatečného kritéria. V tomto případě musíte použít první dostatečné kritérium pro extrém funkce.
Poznámka 2. Druhé dostatečné kritérium pro extrém funkce nelze použít, i když první derivace neexistuje ve stacionárním bodě (pak neexistuje ani druhá derivace). V tomto případě musíte také použít první dostatečné znaménko extrému funkce.
Lokální povaha extrému funkce
Z výše uvedených definic vyplývá, že extrém funkce je lokální povahy - je to největší a nejmenší hodnota funkce ve srovnání s hodnotami blízkými.
Řekněme, že se díváte na své příjmy za období jednoho roku. Pokud jste v květnu vydělali 45 000 rublů a v dubnu 42 000 rublů a v červnu 39 000 rublů, pak jsou květnové výdělky maximální výdělkové funkce ve srovnání s blízkými hodnotami. Ale v říjnu jste vydělali 71 000 rublů, v září 75 000 rublů a v listopadu 74 000 rublů, takže říjnové výdělky jsou minimem výdělkové funkce ve srovnání s blízkými hodnotami. A můžete snadno vidět, že maximum mezi hodnotami duben-květen-červen je menší než minimum září-říjen-listopad.
Obecně řečeno, na intervalu může mít funkce několik extrémů a může se ukázat, že některé minimum funkce je větší než jakékoli maximum. Takže pro funkci znázorněnou na obrázku výše, .
To znamená, že bychom si neměli myslet, že maximum a minimum funkce jsou její největší a nejmenší hodnoty v celém uvažovaném segmentu. V maximálním bodě má funkce největší hodnotu pouze ve srovnání s těmi hodnotami, které má ve všech bodech dostatečně blízko k maximálnímu bodu, a v minimálním bodě má nejmenší hodnotu pouze ve srovnání s těmito hodnotami. že má ve všech bodech dostatečně blízko minimálnímu bodu.
Proto můžeme objasnit výše uvedený koncept extrémních bodů funkce a nazývat minimální body místní minimální body a maximální body místní maximální body.
Společně hledáme extrémy funkce

Příklad 3
Řešení: Funkce je definovaná a spojitá na celé číselné ose. Jeho derivát ![]() existuje také na celé číselné řadě. Kritickými body jsou tedy v tomto případě pouze ty, ve kterých, tzn. , odkud a . Kritické body a rozdělte celý obor definice funkce do tří intervalů monotonie: . Vyberme v každé z nich jeden řídicí bod a najdeme v tomto bodě znaménko derivace.
existuje také na celé číselné řadě. Kritickými body jsou tedy v tomto případě pouze ty, ve kterých, tzn. , odkud a . Kritické body a rozdělte celý obor definice funkce do tří intervalů monotonie: . Vyberme v každé z nich jeden řídicí bod a najdeme v tomto bodě znaménko derivace.
Pro interval může být kontrolní bod: najít. Vezmeme-li bod v intervalu, dostaneme, a vezmeme-li bod v intervalu, máme. Tedy v intervalech a , a v intervalu . Podle prvního dostatečného kritéria pro extrém neexistuje žádný extrém v bodě (protože derivace si zachovává své znaménko v intervalu) a v bodě má funkce minimum (protože derivace při průchodu mění znaménko z mínus na plus přes tento bod). Pojďme najít odpovídající hodnoty funkce: , a . V intervalu funkce klesá, protože v tomto intervalu , a v intervalu roste, protože v tomto intervalu .
Pro objasnění konstrukce grafu najdeme jeho průsečíky se souřadnicovými osami. Když dostaneme rovnici, jejíž kořeny jsou a , tj. byly nalezeny dva body (0; 0) a (4; 0) grafu funkce. Pomocí všech obdržených informací sestavíme graf (viz začátek příkladu).
Pro samokontrolu během výpočtů můžete použít online derivační kalkulačka .

Příklad 4. Najděte extrémy funkce a sestavte její graf.
Definiční obor funkce je celá číselná osa kromě bodu, tzn. .
Pro zkrácení studia můžete využít toho, že tato funkce je sudá, od r  . Proto je jeho graf symetrický kolem osy Oj a studie může být provedena pouze pro interval.
. Proto je jeho graf symetrický kolem osy Oj a studie může být provedena pouze pro interval.
Hledání derivace ![]() a kritické body funkce:
a kritické body funkce:
1)  ;
;
2) ![]() ,
,
ale funkce v tomto bodě trpí diskontinuitou, takže nemůže být extrémním bodem.
Daná funkce má tedy dva kritické body: a . S ohledem na paritu funkce budeme kontrolovat pouze bod pomocí druhého dostatečného kritéria pro extrém. K tomu najdeme druhou derivaci ![]() a určete jeho znaménko na: dostaneme . Protože a , je to minimální bod funkce a
a určete jeho znaménko na: dostaneme . Protože a , je to minimální bod funkce a ![]() .
.
Abychom získali úplnější obrázek o grafu funkce, zjistěme její chování na hranicích definičního oboru:

(zde symbol označuje touhu X na nulu zprava a X zůstává pozitivní; podobně znamená aspirace X na nulu zleva a X zůstává negativní). Tedy pokud , tak . Dále najdeme
 ,
,
těch. pokud, tak.
Graf funkce nemá žádné průsečíky s osami. Obrázek je na začátku příkladu.
Pro samokontrolu během výpočtů můžete použít online derivační kalkulačka .
Pokračujeme v hledání extrémů funkce společně
Příklad 8. Najděte extrémy funkce.

Řešení. Pojďme najít definiční obor funkce. Protože nerovnost musí být splněna, získáme z .
Pojďme najít první derivaci funkce.
Uvažujme graf spojité funkce y=f(x) znázorněno na obrázku.
Funkční hodnota v bodě X 1 bude větší než funkční hodnoty ve všech sousedních bodech vlevo i vpravo X 1. V tomto případě říkáme, že funkce má v bodě X maximálně 1. Na místě X Funkce 3 má samozřejmě také maximum. Pokud vezmeme v úvahu bod X 2, pak je v něm funkční hodnota menší než všechny sousední hodnoty. V tomto případě říkáme, že funkce má v bodě X 2 minimálně. Stejně tak k věci X 4 .
Funkce y=f(x) na místě X 0 má maximum, pokud je hodnota funkce v tomto bodě větší než její hodnoty ve všech bodech nějakého intervalu obsahujícího bod X 0, tj. pokud existuje takové okolí bodu X 0, což je pro všechny X≠X 0 , příslušnost k této čtvrti, nerovnost platí f(x)<f(x 0 ) .
Funkce y=f(x) Má to minimální na místě X 0 , pokud existuje takové okolí bodu X 0 , to je pro všechny X≠X 0 patřící do tohoto okolí, nerovnost platí f(x)>f(x 0.
Body, ve kterých funkce dosáhne svého maxima a minima, se nazývají extrémní body a hodnoty funkce v těchto bodech se nazývají extrémy funkce.
Věnujme pozornost tomu, že funkce definovaná na segmentu může dosáhnout svého maxima a minima pouze v bodech obsažených v uvažovaném segmentu.
Všimněte si, že pokud má funkce v určitém bodě maximum, neznamená to, že v tomto bodě má funkce největší hodnotu v celé definiční oblasti. Na obrázku diskutovaném výše je funkce v bodě X 1 má maximum, i když existují body, ve kterých jsou funkční hodnoty větší než v bodě X 1 . Zejména, F(X 1) < F(X 4) tj. minimum funkce je větší než maximum. Z definice maxima pouze vyplývá, že se jedná o největší hodnotu funkce v bodech dostatečně blízkých bodu maxima.
Věta 1. (Nezbytná podmínka pro existenci extrému.) Pokud je diferencovatelná funkce y=f(x) má na místě x=x 0 extrém, pak se jeho derivace v tomto bodě stane nulou.
Důkaz. Pro jistotu k bodu X Funkce 0 má maximum. Potom pro dostatečně malé přírůstky Δ X my máme f(x 0 + Δ X)
Přechod v těchto nerovnostech do limitu v Δ X→ 0 a vezmeme-li v úvahu, že derivace F "(X 0) existuje, a proto limita vlevo nezávisí na tom, jak Δ X→ 0, dostaneme: při Δ X → 0 – 0 F"(X 0) ≥ 0 a při A X → 0 + 0 F"(X 0) ≤ 0. Od F"(X 0) definuje číslo, pak jsou tyto dvě nerovnosti konzistentní pouze tehdy, když F"(X 0) = 0.
Osvědčený teorém říká, že maximální a minimální body lze nalézt pouze mezi těmi hodnotami argumentu, při kterých se derivace stává nulou.
Uvažovali jsme případ, kdy funkce má derivaci ve všech bodech určitého segmentu. Jaká je situace v případech, kdy derivát neexistuje? Podívejme se na příklady.
Příklady.
- y=|X|.
Funkce nemá v bodě žádnou derivaci X=0 (v tomto bodě nemá graf funkce definovanou tečnu), ale v tomto bodě má funkce minimum, protože y(0)=0 a pro všechny X≠ 0y > 0.
- Nechat X< x
0 Pak C< x
0 a f "(c)> 0.
Proto f "(c)(x-x 0)<
0 a proto
f(x) - f(x 0 )< 0, tj. f(x)< f(x 0 ).
- Nechat x > x 0 Pak c>x 0 a f" (c)< 0. Prostředek f "(c)(x-x 0)< 0. Proto f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Najděte definiční obor funkce f(x).
- Najděte první derivaci funkce f "(x).
- Určete pro to kritické body:
- najít skutečné kořeny rovnice f "(x)=0;
- najít všechny hodnoty X pro který derivát f "(x) neexistuje.
- Určete znaménko derivace vlevo a vpravo od kritického bodu. Protože znaménko derivace zůstává mezi dvěma kritickými body konstantní, stačí určit znaménko derivace v jednom bodě vlevo a v jednom bodě vpravo od kritického bodu.
- Vypočítejte hodnotu funkce v extrémních bodech.
- Najděte všechny kritické body funkce v intervalu ( a, b) a vypočítejte funkční hodnoty v těchto bodech.
- Vypočítejte hodnoty funkce na koncích segmentu, když x = a, x = b.
- Ze všech získaných hodnot vyberte největší a nejmenší.
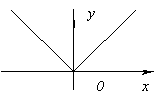
Funkce nemá derivaci at X=0, protože to jde do nekonečna X=0. Ale v tomto okamžiku má funkce maximum.
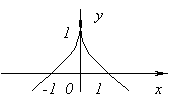
Funkce nemá derivaci at X=0, protože ![]() na X→0. V tomto bodě funkce nemá ani maximum, ani minimum. Opravdu, f(x)=0 a at X<0f(x)<0, а при X>0f(x)>0.
na X→0. V tomto bodě funkce nemá ani maximum, ani minimum. Opravdu, f(x)=0 a at X<0f(x)<0, а при X>0f(x)>0.

Z uvedených příkladů a formulované věty je tedy zřejmé, že funkce může mít extrém pouze ve dvou případech: 1) v bodech, kde derivace existuje a je rovna nule; 2) v bodě, kde derivát neexistuje.
Pokud však v určitém okamžiku X 0 to víme f "(x 0 ) =0, pak z toho nelze usuzovat, že v bodě X 0 funkce má extrém.
Například. ![]() .
.

Ale tečka X=0 není extrémní bod, protože nalevo od tohoto bodu jsou hodnoty funkcí umístěny pod osou Vůl a vpravo nahoře.
Volají se hodnoty argumentu z domény funkce, ve které derivace funkce zaniká nebo neexistuje kritické body.
Ze všeho výše uvedeného vyplývá, že extrémní body funkce patří mezi kritické body a ne každý kritický bod je však extrémním bodem. Chcete-li tedy najít extrém funkce, musíte najít všechny kritické body funkce a poté prozkoumat každý z těchto bodů samostatně na maximum a minimum. K tomuto účelu slouží následující věta.
Věta 2. (Dostatečná podmínka pro existenci extrému.) Nechť je funkce spojitá na nějakém intervalu obsahujícím kritický bod X 0 a je diferencovatelný ve všech bodech tohoto intervalu (snad kromě samotného bodu X 0). Pokud při pohybu zleva doprava přes tento bod derivace změní znaménko z plus na mínus, pak v bodě X = X Funkce 0 má maximum. Pokud, při průjezdu X 0 zleva doprava, derivace změní znaménko z mínus na plus, pak má funkce v tomto bodě minimum.
Pokud tedy
Důkaz. Předpokládejme nejprve, že při průchodu X 0 derivace mění znaménko z plus na mínus, tzn. přede všemi X, blízko k věci X 0 f "(x)> 0 pro X< x 0 , f "(x)< 0 pro x> x 0 Aplikujme na rozdíl Lagrangeovu větu f(x) - f(x 0 ) = f "(c)(x-x 0), kde C leží mezi X A X 0 .
Tedy pro všechny hodnoty X dost blízko X 0 f(x)< f(x 0 ) . A to znamená, že v bodě X Funkce 0 má maximum.
Druhá část věty o minimu je dokázána podobným způsobem.
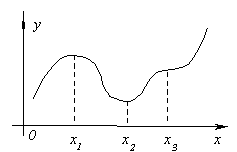
Ukažme si význam této věty na obrázku. Nechat f "(x 1 ) =0 a pro všechny X, dost blízko X 1, nerovnosti jsou splněny
f "(x)< 0 v X< x 1 , f "(x)> 0 v x> x 1 .
Pak doleva od bodu X 1 se funkce zvyšuje a snižuje vpravo, tedy když X = X 1 funkce přechází z rostoucí na klesající, to znamená, že má maximum.
Podobně můžeme uvažovat o bodech X 2 a X 3 .

Vše výše uvedené lze schematicky znázornit na obrázku:
Pravidlo pro studium funkce y=f(x) pro extrém
Příklady. Prozkoumejte funkce pro minimum a maximum.
MAXIMÁLNÍ A NEJMENŠÍ HODNOTY FUNKCE NA Segmentu
Největší hodnota funkce na intervalu je největší ze všech jejích hodnot na tomto intervalu a nejmenší– nejmenší ze všech jeho hodnot.
Zvažte funkci y=f(x) spojitý na segmentu [ a, b]. Jak známo, taková funkce dosahuje svých maximálních a minimálních hodnot buď na hranici segmentu, nebo uvnitř něj. Pokud je největší nebo nejmenší hodnota funkce dosažena ve vnitřním bodě segmentu, pak je tato hodnota maximem nebo minimem funkce, to znamená, že je dosažena v kritických bodech.
Dostáváme tedy následující pravidlo pro nalezení největší a nejmenší hodnoty funkce na segmentu[ a, b] :