Určitý integrál. Jak vypočítat plochu obrázku

Přejděme k aplikacím integrálního počtu. V této lekci analyzujeme typický a nejběžnější úkol - jak použít určitý integrál k výpočtu plochy rovinného obrazce. Konečně ti, kteří hledají smysl ve vyšší matematice – ať ho najdou. Nikdy nevíš. V reálném životě budete muset aproximovat graf dachy pomocí elementárních funkcí a najít jeho plochu pomocí určitého integrálu.

Pro úspěšné zvládnutí materiálu musíte:

1) Porozumět neurčitému integrálu alespoň na středně pokročilé úrovni. Takže figuríny by si měly lekci nejprve přečíst Ne.

2) Umět použít Newton-Leibnizův vzorec a vypočítat určitý integrál. S určitými integrály na stránce můžete navázat vřelé přátelské vztahy Určitý integrál. Příklady řešení.

Ve skutečnosti, abyste našli oblast obrazce, nepotřebujete tolik znalostí o neurčitém a určitém integrálu. Úloha „vypočítat plochu pomocí určitého integrálu“ vždy zahrnuje vytvoření výkresu, takže vaše znalosti a dovednosti v kreslení budou mnohem palčivějším problémem. V tomto ohledu je užitečné osvěžit si paměť grafů základních elementárních funkcí a minimálně umět sestrojit přímku, parabolu a hyperbolu. To lze provést (pro mnohé nutné) pomocí metodického materiálu a článku o geometrických transformacích grafů.

S úkolem najít oblast pomocí určitého integrálu je vlastně každý obeznámen už od školy a my nepůjdeme o moc dál než do školních osnov. Tento článek by možná vůbec neexistoval, ale faktem je, že problém nastává v 99 případech ze 100, kdy student trpí nenáviděnou školou a s nadšením zvládá kurz vyšší matematiky.

Materiály tohoto workshopu jsou prezentovány jednoduše, podrobně as minimem teorie.

Začněme zakřiveným lichoběžníkem.

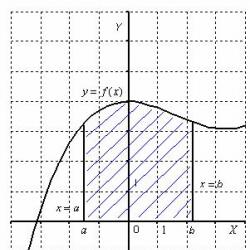
Křivočarý lichoběžník je plochý obrazec ohraničený osou, přímkami a grafem funkce spojité na intervalu, který na tomto intervalu nemění znaménko. Nechte toto číslo lokalizovat ne méně osa x:

Pak plocha křivočarého lichoběžníku se číselně rovná určitému integrálu. Jakýkoli určitý integrál (který existuje) má velmi dobrý geometrický význam. Na lekci Určitý integrál. Příklady řešeníŘekl jsem, že určitý integrál je číslo. A nyní je čas uvést další užitečný fakt. Z hlediska geometrie je určitým integrálem PLOCHA.

to znamená, určitý integrál (pokud existuje) geometricky odpovídá ploše určitého obrazce. Uvažujme například určitý integrál. Integrand definuje křivku v rovině umístěné nad osou (kdo si přeje, může kreslit) a samotný určitý integrál je číselně roven ploše odpovídajícího křivočarého lichoběžníku.

Příklad 1

Toto je typický příkaz k zadání. Prvním a nejdůležitějším bodem při rozhodování je konstrukce výkresu. Kromě toho musí být výkres vytvořen ŽE JO.

Při konstrukci výkresu doporučuji následující pořadí: nejprve je lepší konstruovat všechny přímky (pokud existují) a pouze Pak– paraboly, hyperboly, grafy dalších funkcí. Výhodnější je vytvářet grafy funkcí bod po bodu, techniku ​​výstavby bod po bodu lze nalézt v referenčním materiálu Grafy a vlastnosti elementárních funkcí. Tam také můžete najít velmi užitečný materiál pro naši lekci - jak rychle postavit parabolu.

V tomto problému může řešení vypadat takto.
Dokončíme výkres (všimněte si, že rovnice definuje osu):

Nebudu stínit zakřivený lichoběžník, zde je zřejmé, o jaké oblasti mluvíme. Řešení pokračuje takto:

Na segmentu je umístěn graf funkce nad osou, Proto:

Odpovědět:

Kdo má potíže s výpočtem určitého integrálu a aplikací Newton-Leibnizova vzorce , viz přednáška Určitý integrál. Příklady řešení.

Po dokončení úkolu je vždy užitečné podívat se na nákres a zjistit, zda je odpověď skutečná. V tomto případě počítáme počet buněk ve výkresu „okem“ - no, bude jich asi 9, zdá se, že je to pravda. Je naprosto jasné, že pokud jsme dostali řekněme odpověď: 20 čtverečních jednotek, tak je zřejmé, že se někde stala chyba - 20 buněk se evidentně do dotyčného čísla nevejde, maximálně tucet. Pokud je odpověď záporná, pak byl úkol také vyřešen nesprávně.

Příklad 2

Vypočítejte plochu obrázku ohraničenou čarami , , a osou

Toto je příklad, který můžete vyřešit sami. Úplné řešení a odpověď na konci lekce.

Co dělat, když se nachází zakřivený lichoběžník pod nápravou?

Příklad 3

Vypočítejte plochu obrázku ohraničenou čarami a souřadnicovými osami.

Řešení: Uděláme kresbu:

Pokud je umístěn zakřivený lichoběžník pod nápravou(nebo alespoň ne vyšší daná osa), pak lze její plochu najít pomocí vzorce:
V tomto případě:

Pozornost! Tyto dva typy úkolů by se neměly zaměňovat:

1) Pokud budete požádáni, abyste jednoduše vyřešili určitý integrál bez jakéhokoli geometrického významu, pak může být záporný.

2) Pokud budete požádáni, abyste našli plochu obrazce pomocí určitého integrálu, pak je plocha vždy kladná! Proto se v právě diskutovaném vzorci objevuje mínus.

V praxi se nejčastěji figura nachází v horní i dolní polorovině, a proto od nejjednodušších školních úloh přecházíme k smysluplnějším příkladům.

Příklad 4

Najděte plochu rovinné postavy ohraničenou čarami , .

Řešení: Nejprve musíte dokončit výkres. Obecně řečeno, při konstrukci výkresu v plošných úlohách nás nejvíce zajímají průsečíky čar. Najdeme průsečíky paraboly a přímky. To lze provést dvěma způsoby. První metoda je analytická. Řešíme rovnici:

To znamená, že spodní hranice integrace je , horní hranice integrace je .
Pokud je to možné, je lepší tuto metodu nepoužívat..

Mnohem výnosnější a rychlejší je konstruovat čáry bod po bodu a hranice integrace se vyjasní „samo od sebe“. Technika konstrukce bod po bodu pro různé grafy je podrobně popsána v nápovědě Grafy a vlastnosti elementárních funkcí. Analytická metoda hledání limit se však stále někdy musí použít, pokud je například graf dostatečně velký nebo podrobná konstrukce neodhalila limity integrace (mohou být zlomkové nebo iracionální). A také zvážíme takový příklad.

Vraťme se k našemu úkolu: racionálnější je nejprve sestrojit přímku a teprve potom parabolu. Udělejme nákres:

Opakuji, že při bodové konstrukci se hranice integrace nejčastěji zjišťují „automaticky“.

A nyní pracovní vzorec: Pokud je na segmentu nějaká spojitá funkce větší nebo rovno nějakou spojitou funkci , pak oblast obrázku ohraničenou grafy těchto funkcí a čarami , lze najít pomocí vzorce:

Zde již nemusíte přemýšlet o tom, kde se postava nachází - nad osou nebo pod osou, a zhruba řečeno, záleží, který graf je VYŠŠÍ(vzhledem k jinému grafu), a který je NÍŽE.

V uvažovaném příkladu je zřejmé, že na úsečce se parabola nachází nad přímkou, a proto je nutné odečíst od

Hotové řešení může vypadat takto:

Požadovaná hodnota je omezena parabolou nahoře a přímkou ​​dole.
Na segmentu podle odpovídajícího vzorce:

Odpovědět:

Školní vzorec pro oblast křivočarého lichoběžníku ve spodní polorovině (viz jednoduchý příklad č. 3) je ve skutečnosti speciálním případem vzorce . Protože osa je určena rovnicí a graf funkce je umístěn ne vyšší osy tedy

A nyní pár příkladů pro vlastní řešení

Příklad 5

Příklad 6

Najděte oblast obrázku ohraničenou čarami , .

Při řešení úloh týkajících se výpočtu plochy pomocí určitého integrálu se občas stane vtipná příhoda. Kresba byla provedena správně, výpočty byly správné, ale kvůli neopatrnosti... byla nalezena oblast nesprávného obrázku, přesně takhle to tvůj skromný sluha několikrát podělal. Zde je případ ze skutečného života:

Příklad 7

Vypočítejte plochu obrázku ohraničenou čarami , , , .

Řešení: Nejprve si uděláme kresbu:

...Eh, kresba vypadla, ale vše se zdá být čitelné.

Postava, jejíž oblast potřebujeme najít, je vystínována modře(podívejte se pozorně na stav - jak je počet omezen!). Ale v praxi se kvůli nepozornosti často vyskytuje „závada“, že musíte najít oblast postavy, která je vystínovaná zeleně!

Tento příklad je také užitečný v tom, že počítá plochu obrazce pomocí dvou určitých integrálů. Opravdu:

1) Na segmentu nad osou je graf přímky;

2) Na segmentu nad osou je graf hyperboly.

Je zcela zřejmé, že oblasti mohou (a měly by být) přidány, proto:

Odpovědět:

Přejděme k dalšímu smysluplnému úkolu.

Příklad 8

Vypočítejte plochu obrázku ohraničenou čarami,
Představme rovnice ve „školní“ podobě a nakreslime bod po bodu:

Z nákresu je zřejmé, že naše horní hranice je „dobrá“: .
Ale jaká je spodní hranice?! Je jasné, že to není celé číslo, ale co to je? Možná ? Ale kde je záruka, že je kresba provedena s dokonalou přesností, může se klidně ukázat, že... Nebo kořen. Co když jsme graf sestavili špatně?

V takových případech musíte věnovat více času a analyticky ujasnit limity integrace.

Najdeme průsečíky přímky a paraboly.
Za tímto účelem vyřešíme rovnici:


,

Opravdu, .

Další řešení je triviální, hlavní je nenechat se zmást v substitucích a znacích, výpočty zde nejsou nejjednodušší.

Na segmentu , podle odpovídajícího vzorce:

Odpovědět:

Na závěr lekce se podívejme na dva obtížnější úkoly.

Příklad 9

Vypočítejte plochu obrázku ohraničenou čarami , ,

Řešení: Znázorněme tuto postavu na výkresu.

Sakra, zapomněl jsem podepsat rozvrh a promiň, nechtěl jsem ten obrázek předělávat. Není den kreslení, zkrátka dnes je ten den =)

Pro konstrukci bodu po bodu je nutné znát vzhled sinusoidy (a obecně je užitečné znát grafy všech elementárních funkcí), stejně jako některé sinusové hodnoty, lze je nalézt v trigonometrická tabulka. V některých případech (jako v tomto případě) je možné sestrojit schematický výkres, na kterém by měly být grafy a limity integrace zásadně správně zobrazeny.

Nejsou zde žádné problémy s limity integrace, které vyplývají přímo z podmínky: „x“ se změní z nuly na „pi“. Udělejme další rozhodnutí:

Na segmentu je graf funkce umístěn nad osou, proto:

Jakýkoli určitý integrál (který existuje) má velmi dobrý geometrický význam. Ve třídě jsem řekl, že určitý integrál je číslo. A nyní je čas uvést další užitečný fakt. Z hlediska geometrie je určitým integrálem PLOCHA.

to znamená, určitý integrál (pokud existuje) geometricky odpovídá ploše určitého obrazce. Uvažujme například určitý integrál. Integrand definuje určitou křivku v rovině (v případě potřeby ji lze vždy nakreslit) a samotný určitý integrál je číselně roven ploše odpovídajícího křivočarého lichoběžníku.

Příklad 1

Toto je typický příkaz k zadání. Prvním a nejdůležitějším bodem při rozhodování je konstrukce výkresu. Kromě toho musí být výkres vytvořen ŽE JO.

Při konstrukci výkresu doporučuji následující pořadí: nejprve je lepší konstruovat všechny přímky (pokud existují) a pouze Pak– paraboly, hyperboly, grafy dalších funkcí. Výhodnější je vytvářet grafy funkcí bod po bodu, techniku ​​výstavby bod po bodu lze nalézt v referenčním materiálu.

Tam také můžete najít velmi užitečný materiál pro naši lekci - jak rychle postavit parabolu.

V tomto problému může řešení vypadat takto.
Dokončíme výkres (všimněte si, že rovnice definuje osu):

Nebudu stínit zakřivený lichoběžník, zde je zřejmé, o jaké oblasti mluvíme. Řešení pokračuje takto:

Na segmentu je umístěn graf funkce nad osou, Proto:

Odpovědět:

Kdo má potíže s výpočtem určitého integrálu a aplikací Newton-Leibnizova vzorce , viz přednáška Určitý integrál. Příklady řešení.

Po dokončení úkolu je vždy užitečné podívat se na nákres a zjistit, zda je odpověď skutečná. V tomto případě počítáme počet buněk ve výkresu „okem“ - no, bude jich asi 9, zdá se, že je to pravda. Je naprosto jasné, že pokud jsme dostali řekněme odpověď: 20 čtverečních jednotek, tak je zřejmé, že se někde stala chyba - 20 buněk se evidentně do dotyčného čísla nevejde, maximálně tucet. Pokud je odpověď záporná, pak byl úkol také vyřešen nesprávně.

Příklad 2

Vypočítejte plochu obrázku ohraničenou čarami , , a osou

Toto je příklad, který můžete vyřešit sami. Úplné řešení a odpověď na konci lekce.

Co dělat, když se nachází zakřivený lichoběžník pod nápravou?

Příklad 3

Vypočítejte plochu obrázku ohraničenou čarami a souřadnicovými osami.

Řešení: Udělejme výkres:

Pokud zakřivený lichoběžník zcela umístěn pod osou, pak jeho oblast lze najít pomocí vzorce:
V tomto případě:

Pozornost! Tyto dva typy úkolů by se neměly zaměňovat:

1) Pokud budete požádáni, abyste jednoduše vyřešili určitý integrál bez jakéhokoli geometrického významu, pak může být záporný.

2) Pokud budete požádáni, abyste našli plochu obrazce pomocí určitého integrálu, pak je plocha vždy kladná! Proto se v právě diskutovaném vzorci objevuje mínus.

V praxi se nejčastěji figura nachází v horní i dolní polorovině, a proto od nejjednodušších školních úloh přecházíme k smysluplnějším příkladům.

Příklad 4

Najděte plochu rovinné postavy ohraničenou čarami , .

Řešení: Nejprve musíte udělat výkres. Obecně řečeno, při konstrukci výkresu v plošných úlohách nás nejvíce zajímají průsečíky čar. Najdeme průsečíky paraboly a přímky. To lze provést dvěma způsoby. První metoda je analytická. Řešíme rovnici:

To znamená, že spodní hranice integrace je , horní hranice integrace je .
Pokud je to možné, je lepší tuto metodu nepoužívat.

Mnohem výnosnější a rychlejší je konstruovat čáry bod po bodu a hranice integrace se vyjasní „samo od sebe“. Technika konstrukce bod po bodu pro různé grafy je podrobně popsána v nápovědě Grafy a vlastnosti elementárních funkcí. Analytická metoda hledání limit se však stále někdy musí použít, pokud je například graf dostatečně velký nebo podrobná konstrukce neodhalila limity integrace (mohou být zlomkové nebo iracionální). A také zvážíme takový příklad.

Vraťme se k našemu úkolu: racionálnější je nejprve sestrojit přímku a teprve potom parabolu. Udělejme nákres:

Opakuji, že při bodové konstrukci se hranice integrace nejčastěji zjišťují „automaticky“.

A nyní pracovní vzorec: Pokud na segmentu existuje nějaká spojitá funkce větší nebo rovno nějakou spojitou funkci, pak lze oblast odpovídajícího obrázku najít pomocí vzorce:

Zde již nemusíte přemýšlet o tom, kde se postava nachází - nad osou nebo pod osou, a zhruba řečeno, záleží, který graf je VYŠŠÍ(vzhledem k jinému grafu), a který je NÍŽE.

V uvažovaném příkladu je zřejmé, že na úsečce se parabola nachází nad přímkou, a proto je nutné odečíst od

Hotové řešení může vypadat takto:

Požadovaná hodnota je omezena parabolou nahoře a přímkou ​​dole.
Na segmentu podle odpovídajícího vzorce:

Odpovědět:

Školní vzorec pro oblast křivočarého lichoběžníku ve spodní polorovině (viz jednoduchý příklad č. 3) je ve skutečnosti speciálním případem vzorce . Jelikož je osa určena rovnicí a graf funkce je umístěn pod osou, pak

A nyní pár příkladů pro vlastní řešení

Příklad 5

Příklad 6

Najděte oblast obrázku ohraničenou čarami , .

Při řešení úloh týkajících se výpočtu plochy pomocí určitého integrálu se občas stane vtipná příhoda. Kresba byla provedena správně, výpočty byly správné, ale kvůli neopatrnosti... byla nalezena oblast nesprávného obrázku, přesně takhle to tvůj skromný sluha několikrát podělal. Zde je případ ze skutečného života:

Příklad 7

Vypočítejte plochu obrázku ohraničenou čarami , , , .

Nejprve si uděláme nákres:

Postava, jejíž oblast potřebujeme najít, je vystínována modře(podívejte se pozorně na stav - jak je počet omezen!). Ale v praxi se kvůli nepozornosti často stává, že musíte najít oblast obrázku, která je vystínovaná zeleně!

Tento příklad je také užitečný, protože počítá plochu obrazce pomocí dvou určitých integrálů. Opravdu:

1) Na segmentu nad osou je graf přímky;

2) Na segmentu nad osou je graf hyperboly.

Je zcela zřejmé, že oblasti mohou (a měly by být) přidány, proto:

Odpovědět:

Příklad 8

Vypočítejte plochu obrázku ohraničenou čarami,
Představme rovnice ve „školní“ podobě a nakreslime bod po bodu:

Z nákresu je zřejmé, že naše horní hranice je „dobrá“: .
Ale jaká je spodní hranice?! Je jasné, že to není celé číslo, ale co to je? Možná ? Ale kde je záruka, že je kresba provedena s dokonalou přesností, může se klidně ukázat, že... Nebo kořen. Co když jsme graf sestavili špatně?

V takových případech musíte věnovat více času a analyticky ujasnit limity integrace.

Najdeme průsečíky přímky a paraboly.
Za tímto účelem vyřešíme rovnici:

Proto, .

Další řešení je triviální, hlavní je nenechat se zmást v substitucích a znacích, výpočty zde nejsou nejjednodušší.

Na segmentu , podle odpovídajícího vzorce:

Odpovědět:

Na závěr lekce se podívejme na dva obtížnější úkoly.

Příklad 9

Vypočítejte plochu obrázku ohraničenou čarami , ,

Řešení: Znázorněme tento obrázek na výkresu.

Chcete-li sestavit výkres bod po bodu, musíte znát vzhled sinusoidy (a obecně je užitečné znát grafy všech elementárních funkcí), stejně jako některé sinusové hodnoty, lze je nalézt v trigonometrická tabulka. V některých případech (jako v tomto případě) je možné sestrojit schematický výkres, na kterém by měly být grafy a limity integrace zásadně správně zobrazeny.

Nejsou zde žádné problémy s limity integrace, které vyplývají přímo z podmínky: „x“ se změní z nuly na „pi“. Udělejme další rozhodnutí:

Na segmentu je graf funkce umístěn nad osou, proto:

(1) V lekci můžete vidět, jak jsou sinusy a kosiny integrovány do lichých mocnin Integrály goniometrických funkcí. To je typická technika, odštípneme jeden sinus.

(2) Ve formuláři používáme hlavní goniometrickou identitu

(3) Změňme proměnnou , pak:

Nové oblasti integrace:

Každý, kdo je se střídáním opravdu špatný, vezměte si prosím ponaučení. Substituční metoda v neurčitém integrálu. Pro ty, kteří úplně nerozumí náhradnímu algoritmu v určitém integrálu, navštivte stránku Určitý integrál. Příklady řešení.

Žádné rande________

Předmět:Křivočarý lichoběžník a jeho plocha b

Cíle lekce: Definujte zakřivený lichoběžník a jeho plochu, naučte se vypočítat plochu zakřiveného lichoběžníku.

BĚHEM lekcí

1. Organizační moment.

Pozdravování žáků, kontrola připravenosti třídy na hodinu, organizace pozornosti žáků, odhalení obecných cílů hodiny a jejího plánu.

2. Fáze kontroly domácích úkolů.

Cíle: Zjistit správnost, úplnost a povědomí o plnění domácích úkolů všemi studenty, identifikovat mezery ve znalostech studentů a metodách činnosti. Určete příčiny obtíží a odstraňte případné nalezené mezery.

3. Fáze aktualizace.

Cíle: zajištění motivace k učení školáků, zařazení do společných aktivit ke stanovení cílů hodiny. Aktualizujte subjektivní zkušenost studentů.

Připomeňme si základní pojmy a vzorce.

Definice. Funkce y=F(x), x (a,b), se nazývá primitivní funkce y=f(x), x (a,b), pokud pro všechny X (a,b) platí rovnost

F (x)=f(x).

Komentář. Li F(X) existuje primitivní funkce pro funkci f(x), pak pro libovolnou konstantu S, F(x)+C je také primitivní pro f(x).

Problém nalezení všech primitivních funkcí funkce f(x) se nazývá integrace a množina všech primitivních funkcí se nazývá neurčitý integrál funkce f(x) Podle dx a je určeno

Probíhají následující vlastnosti:

1 . ;

2 . Li C= Takže Const
;

3 .
.

Komentář. Ve školních matematických kurzech se místo toho nepoužívá termín „neurčitý integrál“, říká se „množina všech primitivních derivací“.

Zde je tabulka neurčitých integrálů.

Příklad 1. Najděte primitivní prvek pro funkci
, procházející bodem M(2;4).

Řešení. Množina všech primitivních funkcí funkce
existuje neurčitý integrál
. Vypočítejme to pomocí vlastností integrálu 1 a 2. My máme:

Zjistili jsme, že množina všech primitivních funkcí je dána rodinou funkcí y=F(x)+C, to je y=x 3 – 2x+C, Kde S– libovolná konstanta.

Vědět, že primitivní prvek prochází bodem M(2;4), dosaďte jeho souřadnice do předchozího výrazu a najděte S.

4=2 3 –2 2+S  S=4–8+4; S=0.

Odpovědět: F(x)=x 3 - 2X- požadovaný primitivní derivát.

4. Formování nových konceptů a metod jednání.

Cíle: Zajistit, aby studenti vnímali, pochopili a zapamatovali si probíranou látku. Zajistit, aby studenti zvládli metody reprodukce studovaného materiálu, podporovat filozofické porozumění osvojovaným pojmům, zákonům, pravidlům a vzorcům. Zjistit správnost a informovanost studentů o probrané látce, identifikovat mezery v primárním porozumění a provádět opravy. Zajistěte, aby studenti korelovali své subjektivní zkušenosti se známkami vědeckého poznání.

Hledání ploch rovinných obrazců

Problém hledání plochy rovinné postavy úzce souvisí s problémem hledání primitivních derivátů (integrace). Konkrétně: oblast křivočarého lichoběžníku omezená grafem funkcey=f(x) (f(x)> 0) rovnéx=a; x=b; y= 0, rovná se rozdílu mezi hodnotami primitivní funkce pro funkciy=f(x) v bodechb AA :

S=F(b)–F(a)

Uveďme definici určitého integrálu.

O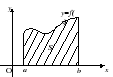
definice. Nechte funkci y=f(x) definované a integrovatelné na intervalu [ a,b] nech to být F(x)- některé jeho prototypy. Potom číslo F(b)–F(a) nazývaný integrál A před b funkcí f(x) a je určeno

.

Rovnost
nazýván Newton-Leibnizův vzorec.

Tento vzorec spojuje problém nalezení plochy rovinné postavy s integrálem.

Obecně platí, že pokud je obrázek omezen funkčními grafy y=f(x);y=g(x) (f(x)>g(x)) a rovnou x=a;x=b, pak se jeho plocha rovná:

.

Příklad 2 V jakém bodě grafu funkce y=x 2 + 1 musíte nakreslit tečnu tak, aby se odřízla od obrazce tvořeného grafem této funkce a přímkami y= 0, x= 0, x= 1 lichoběžník s největší plochou?

Řešení. Nechat M 0 (X 0 ,y 0 ) – bod grafu funkce y=x 2 + 1, ve kterém je zakreslena požadovaná tečna.

Pojďme najít tečnou rovnici y=y 0 +f (X 0 ) (x–x 0 ) .

My máme:

Proto

.

Najděte oblast lichoběžníku OABC.

.

B– průsečík tečny s přímkou x= 1 

Úkol byl zredukován na nalezení největší hodnoty funkce

S(X)=–x 2 +x+ 1 na segmentu. najdeme S (X)=– 2x+ 1. Najděte kritický bod z podmínky S (X)= 0  x=.

Vidíme, že funkce dosahuje své největší hodnoty při x=. najdeme
.

Odpovědět: tečna musí být nakreslena v bodě
.

Všimněte si, že se často setkáváme s problémem hledání integrálu na základě jeho geometrického významu. Ukažme si na příkladu, jak je tento problém vyřešen.

Příklad 4. Pomocí geometrického významu integrálu vypočítejte

A )
; b)
.

Řešení.

A)
- rovná se ploše křivočarého lichoběžníku ohraničeného čarami.

P pojďme se transformovat

– horní polovina kruhu se středem R(1;0) a poloměr R= 1.

Proto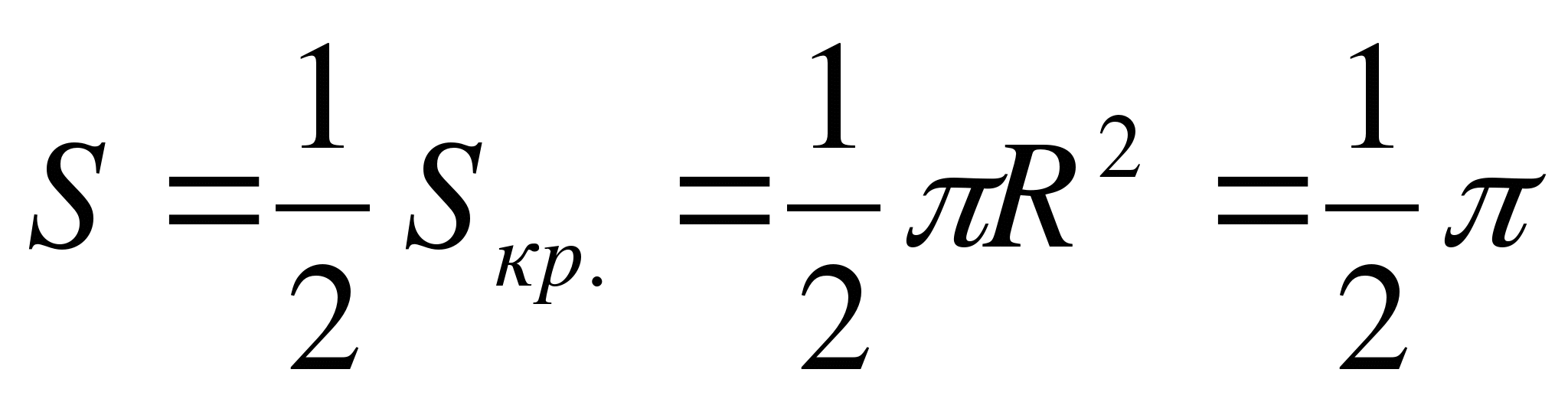
.

Odpovědět:
.

b) Argumentujeme podobně, sestrojme oblast ohraničenou grafy .2 – 2x+ 2, tečný k němu v bodech A
, B(4;2)

y=–9X- 59, parabola y= 3X 2 +ax+ 1, je-li známo, že tečna k parabole v bodě x=– 2 je s osou Vůl velikost úhlu arctg 6.

Nalézt A, pokud je známo, že oblast křivočarého lichoběžníku ohraničená čarami y= 3X 3 + 2x, x=a, y= 0 se rovná jedné.

Najděte nejmenší plochu obrazce ohraničenou parabolou y=x 2 + 2X- 3 a rovný y=kx+ 1.

6. Informační fáze domácích úkolů.

Cíle: Zajistit, aby studenti rozuměli účelu, obsahu a metodám plnění domácích úkolů č. 18, 19,20,21 liché

7. Shrnutí lekce.

Cíl: Poskytnout kvalitativní hodnocení práce třídy i jednotlivých studentů.

Příklad1 . Vypočítejte plochu obrazce ohraničenou přímkami: x + 2y – 4 = 0, y = 0, x = -3 a x = 2

Sestrojme obrazec (viz obrázek) Sestrojíme přímku x + 2y – 4 = 0 pomocí dvou bodů A(4;0) a B(0;2). Vyjádřením y až x dostaneme y = -0,5x + 2. Pomocí vzorce (1), kde f(x) = -0,5x + 2, a = -3, b = 2, zjistíme

S = = [-0,25=11,25 sq. Jednotky

Příklad 2 Vypočítejte plochu obrazce ohraničenou přímkami: x – 2y + 4 = 0, x + y – 5 = 0 a y = 0.

Řešení. Pojďme sestavit postavu.

Sestrojme přímku x – 2y + 4 = 0: y = 0, x = - 4, A(-4; 0); x = 0, y = 2, B(0; 2).

Sestrojme přímku x + y – 5 = 0: y = 0, x = 5, C(5; 0), x = 0, y = 5, D(0; 5).

Pojďme najít průsečík přímek řešením soustavy rovnic:

x = 2, y = 3; M(2; 3).

Pro výpočet požadované plochy rozdělíme trojúhelník AMC na dva trojúhelníky AMN a NMC, protože když se x změní z A na N, je plocha omezena přímkou ​​a když se x změní z N na C - přímkou

Pro trojúhelník AMN máme: ; y = 0,5x + 2, tj. f(x) = 0,5x + 2, a = -4, b = 2.

Pro trojúhelník NMC platí: y = - x + 5, tj. f(x) = - x + 5, a = 2, b = 5.

Výpočtem plochy každého trojúhelníku a sečtením výsledků zjistíme:

sq Jednotky

sq Jednotky

9 + 4, 5 = 13,5 čtverečních. Jednotky Zkontrolujte: = 0,5 AC = 0,5 čtverečních. Jednotky

Příklad 3 Vypočítejte plochu obrázku ohraničenou čarami: y = x 2 , y = 0, x = 2, x = 3.

V tomto případě musíte vypočítat plochu zakřiveného lichoběžníku ohraničeného parabolou y = x 2 , přímky x = 2 a x = 3 a osa Ox (viz obrázek) Pomocí vzorce (1) najdeme plochu křivočarého lichoběžníku

= = 6 čtverečních Jednotky

Příklad 4. Vypočítejte plochu obrázku ohraničenou čarami: y = - x 2 + 4 a y = 0

Pojďme sestavit postavu. Požadovaná plocha je uzavřena mezi parabolou y = - x 2 + 4 a osa Ox.

Najdeme průsečíky paraboly s osou Ox. Za předpokladu, že y = 0, najdeme x = Protože tento údaj je symetrický kolem osy Oy, vypočítáme plochu obrázku umístěného napravo od osy Oy a zdvojnásobíme získaný výsledek: = +4x]sq. Jednotky 2 = 2 čtvereční Jednotky

Příklad 5. Vypočítejte plochu obrazce ohraničenou čarami: y 2 = x, yx = 1, x = 4

Zde musíte vypočítat plochu křivočarého lichoběžníku ohraničeného horní větví paraboly 2 = x, osa Ox a přímky x = 1 a x = 4 (viz obrázek)

Podle vzorce (1), kde f(x) = a = 1 a b = 4, máme = (= čtverečních jednotek.

Příklad 6 . Vypočítejte plochu obrázku ohraničenou čarami: y = sinx, y = 0, x = 0, x= .

Potřebná plocha je omezena půlvlnou sinusoidy a osou Ox (viz obrázek).

Máme - cosx = - cos = 1 + 1 = 2 čtvereční. Jednotky

Příklad 7. Vypočítejte plochu obrázku ohraničenou čarami: y = - 6x, y = 0 a x = 4.

Obrázek je umístěn pod osou Ox (viz obrázek).

Proto zjistíme jeho plochu pomocí vzorce (3)

= =

Příklad 8. Vypočítejte plochu obrazce ohraničenou úsečkami: y = a x = 2. Sestrojte z bodů křivku y = (viz obrázek). Najdeme tedy plochu obrázku pomocí vzorce (4)

Příklad 9 .

X 2 + y 2 = r 2 .

Zde je třeba vypočítat plochu ohraničenou kružnicí x 2 + y 2 = r 2 , tj. oblast kruhu o poloměru r se středem v počátku. Pojďme najít čtvrtou část této oblasti tak, že vezmeme hranice integrace od 0

před; my máme: 1 = = [

Proto, 1 =

Příklad 10. Vypočítejte obsah obrazce ohraničeného čarami: y= x 2 a y = 2x

Toto číslo je omezeno parabolou y = x 2 a přímka y = 2x (viz obrázek) Pro určení průsečíků daných přímek řešíme soustavu rovnic: x 2 – 2x = 0 x = 0 a x = 2

Pomocí vzorce (5) k nalezení oblasti získáme

= \- -fl -- Г -1-±Л_ 1V1 -l-l-Ii-^ 3) |_ 2 3V 2 / J 3 24 24* Příklad 2. Vypočítejme oblast omezenou sinusoidou y = sinXy, Ox osy a přímky (obr. .87). Použitím vzorce (I) dostaneme A 2 S= J sinxdx= [-cos x]Q =0 -(-1) = lf Příklad 3. Vypočítejte plochu ohraničenou obloukem sinusoidy ^у = sin jc, uzavřený mezi dvěma sousedními průsečíky s osou Ox (například mezi počátkem a bodem s úsečkou i). Všimněte si, že z geometrických úvah je jasné, že tato plocha bude dvakrát větší než plocha předchozího příkladu. Udělejme však výpočty: I 5= | s\nxdx= [ - cosх)* - - cos i-(-cos 0)= 1 + 1 = 2. o Náš předpoklad se skutečně ukázal jako správný. Příklad 4. Vypočítejte plochu ohraničenou sinusoidou a osou Ox v jedné periodě (obr. 88). Předběžné výpočty naznačují, že plocha bude čtyřikrát větší než v příkladu 2. Po provedení výpočtů však dostaneme „i Г,*i S - \ sin x dx = [ - cos x]0 = = - cos 2l -( -cos 0) = - 1 + 1 = 0. Tento výsledek vyžaduje upřesnění. Pro objasnění podstaty věci vypočítáme ještě plochu ohraničenou stejnou sinusoidou y = sin l: a osou Ox v rozsahu od l do 2i. Použitím vzorce (I) získáme 2l $2l sin xdx=[ - cosх]l = -cos 2i~)-c05i=- 1-1 =-2. Vidíme tedy, že tato oblast dopadla negativně. Porovnáním s plochou vypočítanou ve cvičení 3 zjistíme, že jejich absolutní hodnoty jsou stejné, ale znaménka se liší. Pokud použijeme vlastnost V (viz kapitola XI, § 4), dostaneme 2l I 2l J sin xdx= J sin * dx [ sin x dx = 2 + (- 2) = 0To, co se stalo v tomto příkladu, není náhoda. Vždy plocha nacházející se pod osou Ox, za předpokladu, že se nezávislá proměnná mění zleva doprava, se získá při výpočtu pomocí integrálů. V tomto kurzu budeme vždy zvažovat oblasti bez značek. Proto bude odpověď v právě probíraném příkladu: požadovaná plocha je 2 + |-2| = 4. Příklad 5. Vypočítejme plochu BAB znázorněnou na Obr. 89. Tato oblast je omezena osou Ox, parabolou y = - xr a přímkou ​​y - = -x+\. Plocha křivočarého lichoběžníku Požadovaná plocha OAB se skládá ze dvou částí: OAM a MAV. Protože bod A je průsečíkem paraboly a přímky, zjistíme jeho souřadnice řešením soustavy rovnic 3 2 Y = mx. (potřebujeme pouze najít úsečku bodu A). Při řešení soustavy najdeme l; = ~. Plochu je proto nutné vypočítat po částech, první čtverec. OAM a pak pl. MAV: .... G 3 2, 3 G xP 3 1/2 U 2. QAM-^x)