Funkcijas ekstrēma. Funkcijas ekstrēmums Palielinošā un samazinošā funkcija
Izmantojot šo pakalpojumu, jūs varat atrast funkcijas lielāko un mazāko vērtību viens mainīgais f(x) ar Word formatētu risinājumu. Ja ir dota funkcija f(x,y), tad jāatrod divu mainīgo funkcijas ekstrēmi. Varat arī atrast funkciju palielināšanas un samazināšanas intervālus.
Noteikumi funkciju ievadīšanai:
Nepieciešamais nosacījums viena mainīgā funkcijas ekstrēmam
Vienādojums f" 0 (x *) = 0 ir nepieciešams nosacījums viena mainīgā funkcijas ekstrēmam, t.i., punktā x * ir jāpazūd funkcijas pirmajam atvasinājumam. Tas identificē stacionārus punktus x c, kuros funkcija nedarbojas. palielināt vai samazināt.Pietiekams nosacījums viena mainīgā funkcijas galējībai
Pieņemsim, ka f 0 (x) ir divreiz diferencējams attiecībā pret x, kas pieder kopai D. Ja punktā x * nosacījums ir izpildīts:F" 0 (x *) = 0
f"" 0 (x *) > 0
Tad punkts x * ir funkcijas lokālais (globālais) minimums.
Ja punktā x * nosacījums ir izpildīts:
F" 0 (x *) = 0
f"" 0 (x *)< 0
Tad punkts x * ir lokālais (globālais) maksimums.
Piemērs Nr.1. Atrodiet funkcijas lielāko un mazāko vērtību: segmentā.
Risinājums. ![]()
Kritiskais punkts ir viens x 1 = 2 (f’(x)=0). Šis punkts pieder segmentam. (Punkts x=0 nav kritisks, jo 0∉).
Mēs aprēķinām funkcijas vērtības segmenta galos un kritiskajā punktā.
f(1)=9, f(2)=5/2, f(3)=38/81
Atbilde: f min = 5/2 pie x=2; f max = 9 pie x = 1
Piemērs Nr.2. Izmantojot augstākas kārtas atvasinājumus, atrodiet funkcijas y=x-2sin(x) ekstrēmu.
Risinājums.
Atrodiet funkcijas atvasinājumu: y’=1-2cos(x) . Atradīsim kritiskos punktus: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. Mēs atrodam y’’=2sin(x), aprēķiniet , kas nozīmē, ka x= π / 3 +2πk, k∈Z ir funkcijas minimālie punkti; ![]() , kas nozīmē x=- π / 3 +2πk, k∈Z ir funkcijas maksimālie punkti.
, kas nozīmē x=- π / 3 +2πk, k∈Z ir funkcijas maksimālie punkti.
Piemērs Nr.3. Izpētīt ekstrēmuma funkciju punkta x=0 tuvumā.
Risinājums. Šeit ir jāatrod funkcijas galējība. Ja ekstremitāte x=0, tad noskaidro tā veidu (minimums vai maksimums). Ja starp atrastajiem punktiem nav x = 0, tad aprēķiniet funkcijas f(x=0) vērtību.
Jāņem vērā, ka tad, kad atvasinājums katrā dotā punkta pusē nemaina savu zīmi, iespējamās situācijas nav izsmeltas pat diferencējamām funkcijām: var gadīties, ka patvaļīgi mazai apkaimei vienā punkta pusē x 0 vai abās pusēs atvasinājuma izmaiņu zīme. Šajos punktos ir nepieciešams izmantot citas metodes, lai pētītu funkcijas ekstremitātē.
Piemērs Nr.4. Sadaliet skaitli 49 divos terminos, kuru reizinājums būs vislielākais.
Risinājums. Apzīmēsim x kā pirmo vārdu. Tad (49-x) ir otrais termins.
Produkts būs maksimālais: x·(49-x) → maks
vai
49 x x 2
Lielākais cilindra tilpums
Atrodiet tā cilindra izmērus ar lielāko tilpumu, kas izgatavots no sagataves lodītes ar rādiusu R formā.Risinājums:

Cilindra tilpums ir: V = πr 2 H
kur H = 2h,
Aizstāsim šīs vērtības mērķa funkcijā.
V → maks
Atradīsim funkcijas ekstrēmu. Tā kā skaļuma funkcija V(h) ir atkarīga tikai no viena mainīgā, atvasinājumu atradīsim, izmantojot pakalpojumu
No šī raksta lasītājs uzzinās par to, kas ir funkcionālās vērtības ekstrēms, kā arī par tā izmantošanas iezīmēm praktiskajās darbībās. Šādas koncepcijas izpēte ir ārkārtīgi svarīga, lai izprastu augstākās matemātikas pamatus. Šī tēma ir būtiska kursa dziļākai izpētei.
Kas ir ekstrēms?
Skolas kursā ir dotas daudzas jēdziena “ekstrēmums” definīcijas. Šis raksts ir paredzēts, lai sniegtu visdziļāko un skaidrāko izpratni par šo terminu tiem, kas šo jautājumu nezina. Tātad termins ir saprotams, cik lielā mērā funkcionālais intervāls iegūst minimālo vai maksimālo vērtību noteiktā kopā.
Ekstrēmums vienlaikus ir gan funkcijas minimālā, gan maksimālā vērtība. Ir minimālais punkts un maksimālais punkts, tas ir, argumenta galējās vērtības grafikā. Galvenās zinātnes, kas izmanto šo jēdzienu, ir:
- statistika;
- mašīnas vadība;
- ekonometrija.
Ekstrēmuma punktiem ir svarīga loma noteiktās funkcijas secības noteikšanā. Koordinātu sistēma grafikā vislabāk parāda galējās pozīcijas izmaiņas atkarībā no funkcionalitātes izmaiņām.
Atvasinātās funkcijas ekstrēma
Ir arī tāda parādība kā “atvasinājums”. Ir nepieciešams noteikt galējo punktu. Ir svarīgi nejaukt minimālos vai maksimālos punktus ar augstāko un zemāko vērtību. Tie ir dažādi jēdzieni, lai gan tie var šķist līdzīgi.
Funkcijas vērtība ir galvenais faktors, kas nosaka, kā atrast maksimālo punktu. Atvasinājums veidojas nevis no vērtībām, bet tikai no tā galējās pozīcijas vienā vai citā secībā.
Pats atvasinājums tiek noteikts, pamatojoties uz šiem galējības punktiem, nevis pēc lielākās vai mazākās vērtības. Krievu skolās robeža starp šiem diviem jēdzieniem nav skaidri novilkta, kas ietekmē izpratni par šo tēmu kopumā.
Tagad aplūkosim tādu jēdzienu kā “akūts ekstremāls”. Mūsdienās pastāv akūta minimālā vērtība un akūta maksimālā vērtība. Definīcija ir dota saskaņā ar Krievijas funkcijas kritisko punktu klasifikāciju. Ekstrēmuma punkta jēdziens ir pamats kritisko punktu atrašanai grafikā.

Lai definētu šādu jēdzienu, viņi izmanto Fermā teorēmu. Tas ir vissvarīgākais ekstremālo punktu izpētē un sniedz skaidru priekšstatu par to esamību vienā vai otrā veidā. Lai nodrošinātu ekstrēmumu, ir svarīgi grafikā radīt noteiktus nosacījumus samazinājumam vai palielinājumam.
Lai precīzi atbildētu uz jautājumu “kā atrast maksimālo punktu”, jums jāievēro šīs vadlīnijas:
- Precīza definīcijas domēna atrašana grafikā.
- Meklējiet funkcijas un ekstrēma punkta atvasinājumu.
- Atrisiniet standarta nevienādības domēnam, kurā tiek atrasts arguments.
- Prast pierādīt, kādās funkcijās punkts grafikā ir definēts un nepārtraukts.

Uzmanību! Funkcijas kritiskā punkta meklēšana iespējama tikai tad, ja ir vismaz otrās kārtas atvasinājums, ko nodrošina liels ekstrēma punkta klātbūtnes īpatsvars.
Nepieciešams nosacījums funkcijas galam
Lai ekstrēms pastāvētu, ir svarīgi, lai būtu gan minimālie, gan maksimālie punkti. Ja šis noteikums tiek ievērots tikai daļēji, tad tiek pārkāpts ekstrēma pastāvēšanas nosacījums.

Katra funkcija jebkurā pozīcijā ir jādiferencē, lai identificētu tās jaunās nozīmes. Ir svarīgi saprast, ka gadījums, kad punkts iet uz nulli, nav galvenais princips, lai atrastu diferencējamu punktu.
Akūts ekstremāls, kā arī funkcijas minimums ir ārkārtīgi svarīgs aspekts matemātiskas problēmas risināšanā, izmantojot ekstrēmas vērtības. Lai labāk izprastu šo komponentu, ir svarīgi atsaukties uz tabulas vērtībām, lai norādītu funkcionalitāti.
| Pilnas nozīmes izpēte | Vērtību diagrammas uzzīmēšana |
| 1. Pieaugošo un samazinošo vērtību punktu noteikšana. 2. Pārrāvumu punktu, galējo punktu un krustpunktu atrašana ar koordinātu asīm. 3. Pozīcijas izmaiņu noteikšanas process grafikā. 4. Izliekuma un izliekuma indikatora un virziena noteikšana, ņemot vērā asimptotu klātbūtni. 5. Pētījuma kopsavilkuma tabulas izveide no tās koordinātu noteikšanas viedokļa. 6. Ekstrēmo un asu punktu pieauguma un samazināšanās intervālu atrašana. 7. Līknes izliekuma un ieliekuma noteikšana. 8. Grafika uzzīmēšana, ņemot vērā pētījumu, ļauj atrast minimumu vai maksimumu. |
Galvenais elements, kad nepieciešams strādāt ar ekstremāliem punktiem, ir tā grafika precīza uzbūve. Skolu skolotāji nereti pievērš maksimālu uzmanību tik svarīgam aspektam, kas ir rupjš izglītības procesa pārkāpums. Grafika konstruēšana notiek tikai pamatojoties uz funkcionālo datu izpētes rezultātiem, identificējot akūtu ekstrēmu, kā arī diagrammas punktus. Atvasinātās funkcijas asās ekstrēmas tiek parādītas precīzu vērtību diagrammā, izmantojot standarta procedūru asimptotu noteikšanai. Funkcijas maksimālo un minimālo punktu pavada sarežģītākas grafiku konstrukcijas. Tas ir saistīts ar dziļāku nepieciešamību risināt akūtu ekstremitāšu problēmu. Ir arī jāatrod sarežģītas un vienkāršas funkcijas atvasinājums, jo tas ir viens no svarīgākajiem jēdzieniem ekstrēma problēmā. |
Funkcionālā galējība
Lai atrastu iepriekš minēto vērtību, jums jāievēro šādi noteikumi:
- noteikt nepieciešamo nosacījumu ekstrēmām attiecībām;
- ņem vērā grafikas galējo punktu pietiekamu stāvokli;
- veikt akūtas ekstremitātes aprēķinu.
Tiek izmantoti arī tādi jēdzieni kā vājš minimums un stiprais minimums. Tas ir jāņem vērā, nosakot ekstrēmu un tā precīzu aprēķinu. Tajā pašā laikā akūtā funkcionalitāte ir visu nepieciešamo apstākļu meklēšana un radīšana darbam ar funkcijas grafiku.
Šī ir diezgan interesanta matemātikas sadaļa, ar kuru saskaras absolūti visi absolventi un studenti. Tomēr ne visiem patīk matāns. Daži nevar saprast pat tādas pamata lietas kā šķietami standarta funkciju pētījums. Šis raksts ir paredzēts, lai labotu šādu kļūdu. Vai vēlaties uzzināt vairāk par funkciju analīzi? Vai vēlaties uzzināt, kas ir ekstremālie punkti un kā tos atrast? Tad šis raksts ir paredzēts jums.
Funkcijas grafika izpēte
Pirmkārt, ir vērts saprast, kāpēc jums vispār ir jāanalizē grafiks. Ir vienkāršas funkcijas, kuras nav grūti uzzīmēt. Spilgts šādas funkcijas piemērs ir parabola. Grafiku uzzīmēt nebūs grūti. Viss, kas nepieciešams, ir, izmantojot vienkāršu transformāciju, lai atrastu skaitļus, pie kuriem funkcija iegūst vērtību 0. Un principā tas ir viss, kas jums jāzina, lai uzzīmētu parabolas grafiku.
Bet ko darīt, ja funkcija, kas mums jāgrafē, ir daudz sarežģītāka? Tā kā sarežģītu funkciju īpašības nav gluži acīmredzamas, ir jāveic visa analīze. Tikai pēc tam funkciju var attēlot grafiski. Kā to izdarīt? Atbildi uz šo jautājumu varat atrast šajā rakstā.
Funkciju analīzes plāns
Pirmā lieta, kas mums jādara, ir veikt virspusēju funkcijas izpēti, kuras laikā mēs atrodam definīcijas jomu. Tātad, sāksim secībā. Definīcijas domēns ir vērtību kopa, ar kuru palīdzību tiek definēta funkcija. Vienkārši sakot, šie ir skaitļi, kurus var izmantot funkcijā x vietā. Lai noteiktu darbības jomu, jums vienkārši jāaplūko ieraksts. Piemēram, ir acīmredzams, ka funkcijai y (x) = x 3 + x 2 - x + 43 ir definīcijas domēns, kas ir reālo skaitļu kopa. Nu, ar tādu funkciju kā (x 2 - 2x)/x viss ir nedaudz savādāk. Tā kā saucējā esošais skaitlis nedrīkst būt vienāds ar 0, šīs funkcijas definīcijas domēns būs visi reālie skaitļi, izņemot nulli.
Tālāk jums jāatrod tā sauktās funkcijas nulles. Šīs ir argumentu vērtības, pie kurām visa funkcija iegūst nulles vērtību. Lai to izdarītu, funkcija ir jāpielīdzina nullei, rūpīgi jāapsver un jāveic dažas transformācijas. Ņemsim jau pazīstamo funkciju y(x) = (x 2 - 2x)/x. No skolas kursa mēs zinām, ka daļa ir vienāda ar 0, ja skaitītājs ir vienāds ar nulli. Tāpēc mēs atmetam saucēju un sākam strādāt ar skaitītāju, pielīdzinot to nullei. Mēs iegūstam x 2 - 2x = 0 un izliekam x no iekavām. Tādējādi x (x - 2) = 0. Rezultātā mēs atklājam, ka mūsu funkcija ir vienāda ar nulli, kad x ir 0 vai 2.
Pētot funkcijas grafiku, daudzi cilvēki saskaras ar problēmām ekstremālo punktu veidā. Un tas ir dīvaini. Galu galā galējības ir diezgan vienkārša tēma. Netici man? Pārliecinies pats, izlasot šo raksta daļu, kurā mēs runāsim par minimālajiem un maksimālajiem punktiem.

Pirmkārt, ir vērts saprast, kas ir ekstrēms. Ekstrēmums ir robežvērtība, ko funkcija sasniedz grafikā. Izrādās, ka ir divas galējās vērtības - maksimālā un minimālā. Skaidrības labad varat apskatīt attēlu augstāk. Pētītajā apgabalā punkts -1 ir funkcijas y (x) = x 5 - 5x maksimums, un punkts 1 attiecīgi ir minimums.
Tāpat nejauciet jēdzienus. Funkcijas galējie punkti ir tie argumenti, pie kuriem dotā funkcija iegūst galējās vērtības. Savukārt ekstrēmums ir funkcijas minimumu un maksimumu vērtība. Piemēram, vēlreiz apsveriet iepriekš minēto attēlu. -1 un 1 ir funkcijas galējie punkti, un 4 un -4 ir paši galējie punkti.
Ekstrēmu punktu atrašana

Bet kā jūs joprojām varat atrast funkcijas galējos punktus? Viss ir pavisam vienkārši. Pirmā lieta, kas jādara, ir atrast vienādojuma atvasinājumu. Pieņemsim, ka esam saņēmuši uzdevumu: “Atrodiet funkcijas y (x) galējos punktus, x ir arguments skaidrības labad ņemsim funkciju y (x) = x 3 + 2x 2 + x + 54. Atšķirsim un. iegūstiet šādu vienādojumu: 3x 2 + 4x + 1. Rezultātā mums ir tikai standarta kvadrātvienādojums, kas ir jāpielīdzina nullei un jāatrod saknes, jo diskriminants ir lielāks par nulli = 16 - 12 = 4), šo vienādojumu nosaka divas saknes: 1/3 un -1. Tomēr, kā jūs varat noteikt, kurš ir kurš Kurš punkts ir maksimālais un kurš ir minimums, lai to izdarītu, ir jāņem blakus esošais punkts un jānoskaidro tā vērtība, kas atrodas pa koordinātu līniju pa kreisi? 1. Aizstājiet šo vērtību vienādojumā y(-2) = 12 - 8 + 1 = 5. Rezultātā mēs iegūstam pozitīvu skaitli. Tas nozīmē, ka intervālā no 1/3 līdz -1. Tas savukārt nozīmē, ka intervālos no mīnus bezgalības līdz 1/3 un no -1 līdz plus bezgalībai funkcija samazinās. Tādējādi varam secināt, ka skaitlis 1/3 ir funkcijas minimālais punkts pētītajā intervālā, bet -1 ir maksimālais punkts.

Ir arī vērts atzīmēt, ka vienotajā valsts eksāmenā ir nepieciešams ne tikai atrast ekstremālos punktus, bet arī veikt ar tiem kādu darbību (saskaitīšanu, reizināšanu utt.). Šī iemesla dēļ ir vērts pievērst īpašu uzmanību problēmas apstākļiem. Galu galā neuzmanības dēļ jūs varat zaudēt punktus.
Funkcijas galējais punkts ir punkts funkcijas definīcijas jomā, kurā funkcijas vērtība iegūst minimālo vai maksimālo vērtību. Funkcijas vērtības šajos punktos sauc par funkcijas galējībām (minimālo un maksimālo)..
Definīcija. Punkts x1 funkciju domēns f(x) sauc funkcijas maksimālais punkts , ja funkcijas vērtība šajā punktā ir lielāka par funkcijas vērtībām punktos, kas atrodas pietiekami tuvu tai, kas atrodas pa labi un pa kreisi no tās (tas ir, nevienlīdzība ir spēkā f(x0 ) > f(x 0 + Δ x) x1 maksimums.
Definīcija. Punkts x2 funkciju domēns f(x) sauc funkcijas minimālais punkts, ja funkcijas vērtība šajā punktā ir mazāka par funkcijas vērtībām punktos, kas atrodas pietiekami tuvu tai, kas atrodas pa labi un pa kreisi no tās (tas ir, nevienlīdzība ir spēkā f(x0 ) < f(x 0 + Δ x) ). Šajā gadījumā mēs sakām, ka funkcijai ir punkts x2 minimums.
Teiksim punkts x1 - funkcijas maksimālais punkts f(x) . Pēc tam intervālā līdz x1 funkcija palielinās, tāpēc funkcijas atvasinājums ir lielāks par nulli ( f "(x) > 0 ), un intervālā pēc x1 funkcija samazinās, tāpēc funkcijas atvasinājums mazāks par nulli ( f "(x) < 0 ). Тогда в точке x1
Pieņemsim arī, ka punkts x2 - funkcijas minimālais punkts f(x) . Pēc tam intervālā līdz x2 funkcija samazinās, un funkcijas atvasinājums ir mazāks par nulli ( f "(x) < 0 ), а в интервале после x2 funkcija palielinās, un funkcijas atvasinājums ir lielāks par nulli ( f "(x) > 0). Šajā gadījumā arī pie punkta x2 funkcijas atvasinājums ir nulle vai neeksistē.
Fermā teorēma (nepieciešama funkcijas ekstrēma esamības pazīme). Ja punkts x0 - funkcijas galējais punkts f(x), tad šajā punktā funkcijas atvasinājums ir vienāds ar nulli ( f "(x) = 0 ) vai neeksistē.
Definīcija. Tiek izsaukti punkti, kuros funkcijas atvasinājums ir nulle vai neeksistē kritiskie punkti .

1. piemērs. Apskatīsim funkciju.
Punktā x= 0 funkcijas atvasinājums ir nulle, tātad punkts x= 0 ir kritiskais punkts. Tomēr, kā redzams funkcijas grafikā, tas palielinās visā definīcijas jomā, tāpēc punkts x= 0 nav šīs funkcijas galējais punkts.
Tādējādi nosacījumi, ka funkcijas atvasinājums punktā ir vienāds ar nulli vai nepastāv, ir nepieciešami nosacījumi galējībai, bet nav pietiekami, jo var sniegt citus funkciju piemērus, kurām šie nosacījumi ir izpildīti, bet funkcija nav ekstrēma attiecīgajā punktā. Tieši tāpēc jābūt pietiekamiem pierādījumiem, ļaujot spriest, vai konkrētajā kritiskajā punktā ir ekstrēms un kāds tas ir - maksimums vai minimums.
Teorēma (pirmā pietiekamā funkcijas ekstrēma esamības pazīme). Kritiskais punkts x0 f(x) ja, ejot cauri šim punktam, funkcijas atvasinājums maina zīmi un ja zīme mainās no “plus” uz “mīnusu”, tad tas ir maksimālais punkts, un ja no “mīnus” uz “pluss”, tad tas ir minimālais punkts.
Ja tuvu punktam x0 , pa kreisi un pa labi no tā atvasinājums saglabā savu zīmi, tas nozīmē, ka funkcija vai nu tikai samazinās, vai tikai palielinās noteiktā punkta apkārtnē. x0 . Šajā gadījumā punktā x0 nav nekādas galējības.
Tātad, lai noteiktu funkcijas galējos punktus, jums jāveic šādas darbības :
- Atrodiet funkcijas atvasinājumu.
- Pielīdziniet atvasinājumu nullei un nosakiet kritiskos punktus.
- Garīgi vai uz papīra atzīmējiet kritiskos punktus uz skaitļu līnijas un nosakiet funkcijas atvasinājuma zīmes iegūtajos intervālos. Ja atvasinājuma zīme mainās no “plus” uz “mīnus”, tad kritiskais punkts ir maksimālais punkts, un, ja no “mīnus” uz “pluss”, tad minimālais punkts.
- Aprēķiniet funkcijas vērtību galējos punktos.

2. piemērs. Atrodiet funkcijas galējību ![]() .
.
Risinājums. Atradīsim funkcijas atvasinājumu:
Pielīdzināsim atvasinājumu nullei, lai atrastu kritiskos punktus:
![]() .
.
Tā kā jebkurai “x” vērtībai saucējs nav vienāds ar nulli, mēs pielīdzinām skaitītāju nullei:
Ir viens kritisks punkts x= 3. Noteiksim atvasinājuma zīmi intervālos, ko norobežo šis punkts:
diapazonā no mīnus bezgalības līdz 3 - mīnusa zīme, tas ir, funkcija samazinās,
intervālā no 3 līdz plus bezgalībai ir plus zīme, tas ir, funkcija palielinās.
Tas ir, punkts x= 3 ir minimālais punkts.
Atradīsim funkcijas vērtību minimālajā punktā:
Tādējādi tiek atrasts funkcijas galējais punkts: (3; 0), un tas ir minimālais punkts.
Teorēma (otra pietiekamā funkcijas ekstrēma esamības pazīme). Kritiskais punkts x0 ir funkcijas galējais punkts f(x) ja funkcijas otrais atvasinājums šajā punktā nav vienāds ar nulli ( f ""(x) ≠ 0), un ja otrais atvasinājums ir lielāks par nulli ( f ""(x) > 0 ), tad maksimālais punkts un, ja otrais atvasinājums ir mazāks par nulli ( f ""(x) < 0 ), то точкой минимума.
Piezīme 1. Ja punktā x0 Ja pazūd gan pirmais, gan otrais atvasinājums, tad šajā brīdī nav iespējams spriest par ekstrēma esamību pēc otrā pietiekamā kritērija. Šajā gadījumā ir jāizmanto pirmais pietiekams funkcijas galējības kritērijs.
2. piezīme. Funkcijas ekstrēma otrais pietiekams kritērijs nav piemērojams pat tad, ja stacionārā punktā pirmais atvasinājums neeksistē (tad neeksistē arī otrs atvasinājums). Šajā gadījumā ir jāizmanto arī pirmā pietiekamā funkcijas ekstrēma zīme.
Funkcijas galējības lokālais raksturs
No iepriekšminētajām definīcijām izriet, ka funkcijas ekstrēmam ir lokāls raksturs – tā ir lielākā un mazākā funkcijas vērtība, salīdzinot ar tuvējām vērtībām.
Pieņemsim, ka skatāties uz saviem ieņēmumiem viena gada periodā. Ja maijā jūs nopelnījāt 45 000 rubļu, bet aprīlī 42 000 rubļu un jūnijā 39 000 rubļu, tad maija ienākumi ir peļņas funkcijas maksimums salīdzinājumā ar tuvējām vērtībām. Bet oktobrī jūs nopelnījāt 71 000 rubļu, septembrī 75 000 rubļu un novembrī 74 000 rubļu, tāpēc oktobra ienākumi ir peļņas funkcijas minimums, salīdzinot ar tuvējām vērtībām. Un jūs varat viegli redzēt, ka maksimums starp aprīļa-maija-jūnija vērtībām ir mazāks par septembra-oktobra-novembra minimumu.
Vispārīgi runājot, intervālā funkcijai var būt vairākas galējības, un var izrādīties, ka kāds funkcijas minimums ir lielāks par jebkuru maksimumu. Tātad, funkcijai, kas parādīta iepriekš attēlā, .
Tas ir, nevajadzētu domāt, ka funkcijas maksimums un minimums ir attiecīgi tās lielākās un mazākās vērtības visā aplūkojamā segmentā. Maksimālajā punktā funkcijai ir lielākā vērtība tikai salīdzinājumā ar tām vērtībām, kuras tai ir visos punktos pietiekami tuvu maksimālajam punktam, un minimālajā punktā tai ir mazākā vērtība tikai salīdzinājumā ar šīm vērtībām. ka tā visos punktos ir pietiekami tuvu minimālajam punktam.
Tāpēc mēs varam precizēt iepriekš minēto funkcijas ekstremālo punktu jēdzienu un nosaukt minimālos punktus par vietējiem minimālajiem punktiem un maksimālos punktus par vietējiem maksimālajiem punktiem.
Mēs kopā meklējam funkcijas galējības

3. piemērs.
Risinājums: funkcija ir definēta un nepārtraukta visā skaitļu rindā. Tā atvasinājums ![]() eksistē arī visā skaitļu rindā. Tāpēc šajā gadījumā kritiskie punkti ir tikai tie, kuros, t.i. , no kurienes un . Kritiskie punkti un sadaliet visu funkcijas definīcijas jomu trīs monotonības intervālos: . Izvēlēsimies katrā no tiem vienu kontrolpunktu un šajā punktā atradīsim atvasinājuma zīmi.
eksistē arī visā skaitļu rindā. Tāpēc šajā gadījumā kritiskie punkti ir tikai tie, kuros, t.i. , no kurienes un . Kritiskie punkti un sadaliet visu funkcijas definīcijas jomu trīs monotonības intervālos: . Izvēlēsimies katrā no tiem vienu kontrolpunktu un šajā punktā atradīsim atvasinājuma zīmi.
Intervālam kontroles punkts var būt: atrast. Ņemot punktu intervālā, mēs iegūstam, un, ņemot punktu intervālā, mums ir. Tātad, intervālos un , Un intervālā . Atbilstoši pirmajam pietiekamajam ekstrēma kritērijam, punktā nav ekstrēma (jo atvasinājums saglabā savu zīmi intervālā), bet punktā funkcijai ir minimums (jo atvasinājums maina zīmi no mīnusa uz plusu, kad tiek nodota garām caur šo punktu). Atradīsim atbilstošās funkcijas vērtības: , a . Intervālā funkcija samazinās, jo šajā intervālā , un intervālā tā palielinās, jo šajā intervālā .
Lai precizētu grafa uzbūvi, atrodam tā krustošanās punktus ar koordinātu asīm. Iegūstot vienādojumu, kura saknes ir un , t.i., funkcijas grafikā ir atrasti divi punkti (0; 0) un (4; 0). Izmantojot visu saņemto informāciju, mēs veidojam grafiku (skatiet piemēra sākumu).
Pašpārbaudei aprēķinu laikā varat izmantot tiešsaistes atvasinājumu kalkulators .

4. piemērs. Atrodiet funkcijas galējību un izveidojiet tās grafiku.
Funkcijas definīcijas apgabals ir visa skaitļa līnija, izņemot punktu, t.i. .
Lai saīsinātu pētījumu, varat izmantot faktu, ka šī funkcija ir pat, jo  . Tāpēc tā grafiks ir simetrisks pret asi Oy un pētījumu var veikt tikai intervālam.
. Tāpēc tā grafiks ir simetrisks pret asi Oy un pētījumu var veikt tikai intervālam.
Atvasinājuma atrašana ![]() un funkcijas kritiskie punkti:
un funkcijas kritiskie punkti:
1)  ;
;
2) ![]() ,
,
bet šajā brīdī funkcijai ir pārtraukums, tāpēc tas nevar būt galējības punkts.
Tādējādi dotajai funkcijai ir divi kritiskie punkti: un . Ņemot vērā funkcijas paritāti, mēs pārbaudīsim tikai punktu, izmantojot otro pietiekamo ekstrēmuma kritēriju. Lai to izdarītu, mēs atrodam otro atvasinājumu ![]() un noteikt tās zīmi: mēs saņemam . Tā kā un , tas ir funkcijas un minimālais punkts
un noteikt tās zīmi: mēs saņemam . Tā kā un , tas ir funkcijas un minimālais punkts ![]() .
.
Lai iegūtu pilnīgāku priekšstatu par funkcijas grafiku, noskaidrosim tās uzvedību definīcijas apgabala robežās:

(šeit simbols norāda vēlmi x uz nulli no labās puses un x paliek pozitīvs; līdzīgi nozīmē tiekšanos x uz nulli no kreisās puses un x paliek negatīvs). Tādējādi, ja , tad . Tālāk mēs atrodam
 ,
,
tie. ja, tad.
Funkcijas grafikam nav krustošanās punktu ar asīm. Attēls ir piemēra sākumā.
Pašpārbaudei aprēķinu laikā varat izmantot tiešsaistes atvasinājumu kalkulators .
Mēs turpinām kopā meklēt funkcijas galējības
8. piemērs. Atrodiet funkcijas galējību.

Risinājums. Atradīsim funkcijas definīcijas apgabalu. Tā kā nevienlīdzība ir jāapmierina, mēs iegūstam no .
Atradīsim funkcijas pirmo atvasinājumu.
Apsveriet nepārtrauktas funkcijas grafiku y=f(x) parādīts attēlā.
Funkcijas vērtība punktā x 1 būs lielākas par funkciju vērtībām visos blakus punktos gan pa kreisi, gan pa labi no x 1. Šajā gadījumā mēs sakām, ka funkcijai ir punkts x 1 maksimums. Punktā x Acīmredzot 3. funkcijai ir arī maksimums. Ja ņemam vērā būtību x 2, tad funkcijas vērtība tajā ir mazāka par visām blakus vērtībām. Šajā gadījumā mēs sakām, ka funkcijai ir punkts x 2 minimums. Tāpat par punktu x 4 .
Funkcija y=f(x) punktā x 0 ir maksimums, ja funkcijas vērtība šajā punktā ir lielāka par tās vērtībām visos intervāla punktos, kas satur punktu x 0, t.i. ja ir tāda punkta apkārtne x 0, kas ir visiem x≠x 0 , piederība šai apkaimē, nevienlīdzība pastāv f(x)<f(x 0 ) .
Funkcija y=f(x) ir minimums punktā x 0 , ja ir tāda punkta apkārtne x 0 , tas ir visiem x≠x 0, kas pieder šai apkārtnei, pastāv nevienlīdzība f(x)>f(x 0.
Punktus, kuros funkcija sasniedz maksimumu un minimumu, sauc par ekstremālajiem punktiem, un funkcijas vērtības šajos punktos sauc par funkcijas galējībām.
Pievērsīsim uzmanību tam, ka segmentā definēta funkcija savu maksimumu un minimumu var sasniegt tikai apskatāmā segmenta punktos.
Ņemiet vērā: ja funkcijai kādā punktā ir maksimums, tas nenozīmē, ka tajā brīdī funkcijai ir vislielākā vērtība visā definīcijas jomā. Iepriekš apskatītajā attēlā funkcija punktā x 1 ir maksimums, lai gan ir punkti, kuros funkcijas vērtības ir lielākas nekā punktā x 1 . Jo īpaši f(x 1) < f(x 4) t.i. funkcijas minimums ir lielāks par maksimumu. No maksimuma definīcijas tikai izriet, ka šī ir lielākā funkcijas vērtība punktos, kas ir pietiekami tuvu maksimālajam punktam.
Teorēma 1. (Nepieciešams nosacījums ekstrēma esamībai.) Ja diferencējamā funkcija y=f(x) ir punktā x=x 0 ekstrēmu, tad tā atvasinājums šajā punktā kļūst par nulli.
Pierādījums. Ļaujiet, lai noteiktu, pie punkta x 0 funkcijai ir maksimums. Tad pietiekami maziem soļiem Δ x mums ir f(x 0 + Δ x)
Šo nevienādību pāreja uz robežu pie Δ x→ 0 un ņemot vērā, ka atvasinājums f "(x 0) pastāv, un tāpēc ierobežojums kreisajā pusē nav atkarīgs no tā, kā Δ x→ 0, mēs iegūstam: pie Δ x → 0 – 0 f"(x 0) ≥ 0 a pie Δ x → 0 + 0 f"(x 0) ≤ 0. Kopš f"(x 0) definē skaitli, tad šīs divas nevienādības ir savietojamas tikai tad, ja f"(x 0) = 0.
Pierādītā teorēma nosaka, ka maksimālo un minimālo punktu var atrast tikai starp tām argumenta vērtībām, pie kurām atvasinājums kļūst par nulli.
Mēs aplūkojām gadījumu, kad funkcijai ir atvasinājums visos noteikta segmenta punktos. Kāda ir situācija gadījumos, kad atvasinājums nepastāv? Apskatīsim piemērus.
Piemēri.
- y=|x|.
Funkcijai punktā nav atvasinājuma x=0 (šajā brīdī funkcijas grafikam nav noteiktas pieskares), bet šajā brīdī funkcijai ir minimums, jo y(0)=0 un visiem x≠ 0y > 0.
- Ļaujiet x< x
0 . Tad c< x
0 un f "(c)> 0.
Tieši tāpēc f "(c)(x-x 0)<
0 un tāpēc
f(x) - f(x 0 )< 0, t.i. f(x)< f(x 0 ).
- Ļaujiet x > x 0 . Tad c>x 0 un f "(c)< 0. Līdzekļi f "(c)(x-x 0)< 0. Tieši tāpēc f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Atrodiet funkcijas domēnu f(x).
- Atrodiet funkcijas pirmo atvasinājumu f "(x).
- Nosakiet tam kritiskos punktus:
- atrodiet vienādojuma īstās saknes f "(x)=0;
- atrast visas vērtības x kuriem atvasinājums f "(x) neeksistē.
- Nosakiet atvasinājuma zīmi pa kreisi un pa labi no kritiskā punkta. Tā kā starp diviem kritiskajiem punktiem atvasinājuma zīme paliek nemainīga, pietiek ar atvasinājuma zīmi noteikt vienā punktā pa kreisi un vienu punktu pa labi no kritiskā punkta.
- Aprēķiniet funkcijas vērtību galējos punktos.
- Atrodiet visus funkcijas kritiskos punktus intervālā ( a, b) un aprēķiniet funkciju vērtības šajos punktos.
- Aprēķiniet funkcijas vērtības segmenta galos, kad x = a, x = b.
- No visām iegūtajām vērtībām atlasiet lielāko un mazāko.
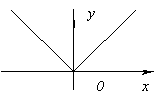
Funkcijai nav atvasinājuma at x=0, jo tas iet līdz bezgalībai pie x=0. Bet šajā brīdī funkcijai ir maksimums.
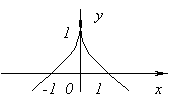
Funkcijai nav atvasinājuma at x=0, kopš ![]() plkst x→0. Šajā brīdī funkcijai nav ne maksimuma, ne minimuma. Tiešām, f(x)=0 un plkst x<0f(x)<0, а при x>0f(x)>0.
plkst x→0. Šajā brīdī funkcijai nav ne maksimuma, ne minimuma. Tiešām, f(x)=0 un plkst x<0f(x)<0, а при x>0f(x)>0.

Tādējādi no dotajiem piemēriem un formulētās teorēmas ir skaidrs, ka funkcijai ekstrēmums var būt tikai divos gadījumos: 1) punktos, kur atvasinājums eksistē un ir vienāds ar nulli; 2) vietā, kur atvasinājums nepastāv.
Tomēr, ja kādā brīdī x 0 mēs to zinām f "(x 0 ) =0, tad no tā nevar secināt, ka punktā x 0 funkcijai ir ekstrēmums.
Piemēram. ![]() .
.

Bet punkts x=0 nav galējais punkts, jo pa kreisi no šī punkta funkcijas vērtības atrodas zem ass Vērsis, un augšpusē labajā pusē.
Argumenta vērtības no funkcijas domēna, kurā funkcijas atvasinājums pazūd vai nepastāv, tiek sauktas kritiskie punkti.
No visa iepriekš minētā izriet, ka funkcijas galējie punkti ir starp kritiskajiem punktiem, un tomēr ne katrs kritiskais punkts ir galējais punkts. Tāpēc, lai atrastu funkcijas galējību, ir jāatrod visi funkcijas kritiskie punkti un pēc tam jāpārbauda katrs no šiem punktiem atsevišķi maksimālajam un minimumam. Šim nolūkam kalpo šāda teorēma.
Teorēma 2. (Pietiekams nosacījums ekstrēma pastāvēšanai.) Lai funkcija ir nepārtraukta kādā intervālā, kas satur kritisko punktu x 0, un ir diferencējams visos šī intervāla punktos (izņemot, iespējams, pašu punktu x 0). Ja, pārvietojoties no kreisās puses uz labo caur šo punktu, atvasinājums maina zīmi no plusa uz mīnusu, tad punktā x = x 0 funkcijai ir maksimums. Ja, ejot cauri x 0 no kreisās puses uz labo, atvasinājums maina zīmi no mīnusa uz plusu, tad funkcijai šajā brīdī ir minimums.
Tādējādi, ja
Pierādījums. Vispirms pieņemsim, ka, ejot cauri x 0 atvasinājums maina zīmi no plus uz mīnusu, t.i. visu priekšā x, tuvu punktam x 0 f "(x)> 0 par x< x 0 , f "(x)< 0 par x>x 0 . Atšķirībai piemērosim Lagranža teorēmu f(x) - f(x 0 ) = f "(c)(x-x 0), kur c atrodas starp x Un x 0 .
Tādējādi visām vērtībām x pietiekami tuvu x 0 f(x)< f(x 0 ) . Un tas nozīmē, ka brīdī x 0 funkcijai ir maksimums.
Minimālās teorēmas otrā daļa ir pierādīta līdzīgi.
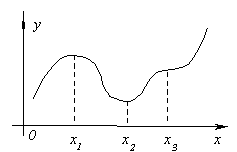
Ilustrēsim šīs teorēmas nozīmi attēlā. Ļaujiet f "(x 1 ) =0 un jebkuram x, pietiekami tuvu x 1, nevienādības ir izpildītas
f "(x)< 0 plkst x< x 1 , f "(x)> 0 plkst x>x 1 .
Pēc tam pa kreisi no punkta x 1 funkcija labajā pusē palielinās un samazinās, tāpēc, kad x = x 1 funkcija pāriet no pieaugošas uz samazināšanos, tas ir, tai ir maksimums.
Līdzīgi mēs varam apsvērt punktus x 2 un x 3 .

Visu iepriekš minēto var shematiski attēlot attēlā:
Ekstrēmuma funkcijas y=f(x) izpētes noteikums
Piemēri. Izpētiet minimālās un maksimālās funkcijas.
Segmenta FUNKCIJAS MAKSIMĀLĀS UN MAZĀKĀS VĒRTĪBAS
Lielākais funkcijas vērtība intervālā ir lielākā no visām tās vērtībām šajā intervālā, un mazākais– mazākā no visām tā vērtībām.
Apsveriet funkciju y=f(x) nepārtraukts segmentā [ a, b]. Kā zināms, šāda funkcija sasniedz maksimālo un minimālo vērtību vai nu uz segmenta robežas, vai tā iekšpusē. Ja lielākā vai mazākā funkcijas vērtība tiek sasniegta segmenta iekšējā punktā, tad šī vērtība ir funkcijas maksimālā vai minimālā vērtība, tas ir, tā tiek sasniegta kritiskajos punktos.
Tādējādi mēs iegūstam sekojošo noteikums, lai atrastu funkcijas lielākās un mazākās vērtības segmentā[ a, b] :