Integral definida. Como calcular a área de uma figura

Vamos considerar as aplicações do cálculo integral. Nesta lição analisaremos a tarefa típica e mais comum – como usar uma integral definida para calcular a área de uma figura plana. Finalmente, aqueles que procuram significado na matemática superior - que o encontrem. Nunca se sabe. Na vida real, você terá que aproximar um gráfico de dacha usando funções elementares e encontrar sua área usando uma integral definida.

Para dominar o material com sucesso, você deve:

1) Compreender a integral indefinida pelo menos num nível intermédio. Assim, os manequins devem primeiro ler a lição Não.

2) Ser capaz de aplicar a fórmula de Newton-Leibniz e calcular a integral definida. Você pode estabelecer relações calorosas e amigáveis com certas integrais na página Integral definida. Exemplos de soluções.

Na verdade, para encontrar a área de uma figura, você não precisa de tanto conhecimento sobre integral indefinida e definida. A tarefa “calcular a área usando uma integral definida” envolve sempre a construção de um desenho, então seu conhecimento e habilidades de desenho serão uma questão muito mais urgente. A este respeito, é útil refrescar a memória dos gráficos das funções elementares básicas e, no mínimo, ser capaz de construir uma reta, uma parábola e uma hipérbole. Isso pode ser feito (para muitos é necessário) com a ajuda de material metodológico e de um artigo sobre transformações geométricas de gráficos.

Na verdade, todos estão familiarizados com a tarefa de encontrar a área usando uma integral definida desde a escola, e não iremos muito além do currículo escolar. Este artigo pode nem existir, mas o fato é que o problema ocorre em 99 casos em 100, quando um aluno sofre com uma escola odiada e domina com entusiasmo um curso de matemática superior.

Os materiais deste workshop são apresentados de forma simples, detalhada e com um mínimo de teoria.

Vamos começar com um trapézio curvo.

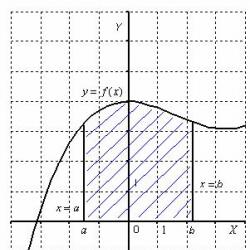
Trapézio curvilíneoé uma figura plana delimitada por um eixo, linhas retas e o gráfico de uma função contínua em um intervalo que não muda de sinal nesse intervalo. Deixe esta figura ser localizada não menos eixo x:

Então a área de um trapézio curvilíneo é numericamente igual a uma integral definida. Qualquer integral definida (que exista) tem um significado geométrico muito bom. Na lição Integral definida. Exemplos de soluções Eu disse que uma integral definida é um número. E agora é hora de expor outro fato útil. Do ponto de vista da geometria, a integral definida é ÁREA.

Aquilo é, a integral definida (se existir) corresponde geometricamente à área de uma determinada figura. Por exemplo, considere a integral definida. O integrando define uma curva no plano localizado acima do eixo (quem quiser pode fazer um desenho), e a própria integral definida é numericamente igual à área do trapézio curvilíneo correspondente.

Exemplo 1

Esta é uma declaração de atribuição típica. O primeiro e mais importante ponto na decisão é a construção de um desenho. Além disso, o desenho deve ser construído CERTO.

Ao construir um desenho, recomendo a seguinte ordem: inicialmenteé melhor construir todas as linhas retas (se existirem) e apenas Então– parábolas, hipérboles, gráficos de outras funções. É mais lucrativo construir gráficos de funções ponto por ponto, a técnica de construção ponto a ponto pode ser encontrada no material de referência Gráficos e propriedades de funções elementares. Lá você também pode encontrar material muito útil para nossa lição - como construir uma parábola rapidamente.

Neste problema, a solução pode ser assim.
Vamos completar o desenho (observe que a equação define o eixo):

Não vou sombrear o trapézio curvo; é óbvio aqui de que área estamos falando. A solução continua assim:

No segmento, o gráfico da função está localizado acima do eixo, É por isso:

Responder:

Quem tem dificuldades em calcular a integral definida e aplicar a fórmula de Newton-Leibniz , consulte a palestra Integral definida. Exemplos de soluções.

Depois de concluída a tarefa, é sempre útil olhar o desenho e descobrir se a resposta é real. Nesse caso, contamos o número de células do desenho “a olho” - bem, serão cerca de 9, parece ser verdade. É absolutamente claro que se obtivermos, digamos, a resposta: 20 unidades quadradas, então é óbvio que foi cometido um erro em algum lugar - 20 células obviamente não cabem no número em questão, no máximo uma dúzia. Se a resposta for negativa, a tarefa também foi resolvida incorretamente.

Exemplo 2

Calcule a área de uma figura delimitada por linhas, e eixo

Este é um exemplo para você resolver sozinho. Solução completa e resposta no final da lição.

O que fazer se o trapézio curvo estiver localizado embaixo do eixo?

Exemplo 3

Calcule a área da figura delimitada por linhas e eixos coordenados.

Solução: Vamos fazer um desenho:

Se um trapézio curvo estiver localizado sob o eixo(ou pelo menos não mais alto dado eixo), então sua área pode ser encontrada usando a fórmula:
Nesse caso:

Atenção! Os dois tipos de tarefas não devem ser confundidos:

1) Se lhe for solicitado que resolva simplesmente uma integral definida sem qualquer significado geométrico, então ela pode ser negativa.

2) Se você for solicitado a encontrar a área de uma figura usando uma integral definida, a área será sempre positiva! É por isso que o sinal de menos aparece na fórmula que acabamos de discutir.

Na prática, na maioria das vezes a figura está localizada no semiplano superior e inferior e, portanto, dos problemas escolares mais simples passamos para exemplos mais significativos.

Exemplo 4

Encontre a área de uma figura plana limitada pelas linhas , .

Solução: Primeiro você precisa completar o desenho. De modo geral, ao construir um desenho em problemas de área, estamos mais interessados nos pontos de intersecção das retas. Vamos encontrar os pontos de intersecção da parábola e da reta. Isso pode ser feito de duas maneiras. O primeiro método é analítico. Resolvemos a equação:

Isso significa que o limite inferior de integração é, o limite superior de integração é.
Se possível, é melhor não usar este método..

É muito mais rentável e rápido construir linhas ponto por ponto, e os limites da integração tornam-se claros “por si próprios”. A técnica de construção ponto a ponto para vários gráficos é discutida em detalhes na ajuda Gráficos e propriedades de funções elementares. No entanto, o método analítico de encontrar limites às vezes ainda tem que ser usado se, por exemplo, o gráfico for grande o suficiente, ou se a construção detalhada não revelar os limites de integração (eles podem ser fracionários ou irracionais). E também consideraremos esse exemplo.

Voltemos à nossa tarefa: é mais racional construir primeiro uma reta e só depois uma parábola. Vamos fazer o desenho:

Repito que na construção pontual, os limites da integração são na maioria das vezes descobertos “automaticamente”.

E agora a fórmula de trabalho: Se houver alguma função contínua no segmento Melhor que ou igual a alguma função contínua , então a área da figura delimitada pelos gráficos dessas funções e pelas retas , , pode ser encontrada usando a fórmula:

Aqui você não precisa mais pensar onde a figura está localizada - acima do eixo ou abaixo do eixo e, grosso modo, importa qual gráfico é MAIOR(em relação a outro gráfico), e qual está ABAIXO.

No exemplo em consideração, é óbvio que no segmento a parábola está localizada acima da reta e, portanto, é necessário subtrair de

A solução completa pode ser assim:

A figura desejada é limitada por uma parábola acima e uma linha reta abaixo.
No segmento, de acordo com a fórmula correspondente:

Responder:

Na verdade, a fórmula escolar para a área de um trapézio curvilíneo no semiplano inferior (ver exemplo simples nº 3) é um caso especial da fórmula . Como o eixo é dado pela equação e o gráfico da função está localizado não mais alto eixos, então

E agora alguns exemplos para sua própria solução

Exemplo 5

Exemplo 6

Encontre a área da figura delimitada pelas linhas , .

Ao resolver problemas que envolvem cálculo de área usando uma integral definida, às vezes acontece um incidente engraçado. O desenho foi feito corretamente, os cálculos estavam corretos, mas por descuido... a área da figura errada foi encontrada, foi exatamente assim que seu humilde servo errou várias vezes. Aqui está um caso da vida real:

Exemplo 7

Calcule a área da figura delimitada pelas linhas , , , .

Solução: Primeiro vamos fazer um desenho:

...Eh, o desenho ficou uma porcaria, mas parece tudo legível.

A figura cuja área precisamos encontrar está sombreada em azul(observe atentamente a condição - como o número é limitado!). Mas, na prática, por desatenção, muitas vezes ocorre uma “falha” de que você precisa encontrar a área de uma figura sombreada em verde!

Este exemplo também é útil porque calcula a área de uma figura usando duas integrais definidas. Realmente:

1) No segmento acima do eixo há um gráfico de uma reta;

2) No segmento acima do eixo está o gráfico de uma hipérbole.

É bastante óbvio que as áreas podem (e devem) ser somadas, portanto:

Responder:

Vamos passar para outra tarefa significativa.

Exemplo 8

Calcule a área de uma figura delimitada por linhas,
Vamos apresentar as equações na forma “escolar” e fazer um desenho ponto a ponto:

Pelo desenho fica claro que nosso limite superior é “bom”: .
Mas qual é o limite inferior?! É claro que este não é um número inteiro, mas o que é? Talvez ? Mas onde está a garantia de que o desenho é feito com perfeita precisão, pode muito bem acontecer que... Ou a raiz. E se construíssemos o gráfico incorretamente?

Nesses casos, é necessário dedicar mais tempo e esclarecer analiticamente os limites da integração.

Vamos encontrar os pontos de intersecção de uma linha reta e uma parábola.
Para fazer isso, resolvemos a equação:

,

Realmente, .

A solução adicional é trivial, o principal é não se confundir com substituições e sinais; os cálculos aqui não são dos mais simples;

No segmento , de acordo com a fórmula correspondente:

Responder:

Bem, para concluir a lição, vejamos mais duas tarefas difíceis.

Exemplo 9

Calcule a área da figura delimitada pelas linhas , ,

Solução: Vamos representar esta figura no desenho.

Droga, esqueci de assinar o cronograma e, desculpe, não queria refazer a foto. Não é dia de desenho, enfim, hoje é dia =)

Para construção ponto a ponto, é necessário conhecer a aparência de uma senóide (e em geral é útil saber gráficos de todas as funções elementares), bem como alguns valores de seno, eles podem ser encontrados em tabela trigonométrica. Em alguns casos (como neste caso), é possível construir um desenho esquemático, no qual os gráficos e limites de integração devem ser apresentados fundamentalmente de forma correta.

Não há problemas com os limites de integração aqui; eles decorrem diretamente da condição: - “x” muda de zero para “pi”. Vamos tomar outra decisão:

No segmento, o gráfico da função está localizado acima do eixo, portanto:

Qualquer integral definida (que exista) tem um significado geométrico muito bom. Na aula eu disse que uma integral definida é um número. E agora é hora de expor outro fato útil. Do ponto de vista da geometria, a integral definida é ÁREA.

Aquilo é, a integral definida (se existir) corresponde geometricamente à área de uma determinada figura. Por exemplo, considere a integral definida. O integrando define uma certa curva no plano (sempre pode ser desenhada se desejado), e a própria integral definida é numericamente igual à área do trapézio curvilíneo correspondente.

Exemplo 1

Esta é uma declaração de atribuição típica. O primeiro e mais importante ponto na decisão é a construção de um desenho. Além disso, o desenho deve ser construído CERTO.

Lá você também pode encontrar material muito útil para nossa lição - como construir uma parábola rapidamente.

Neste problema, a solução pode ser assim.
Vamos completar o desenho (observe que a equação define o eixo):

Não vou sombrear o trapézio curvo; é óbvio aqui de que área estamos falando. A solução continua assim:

No segmento, o gráfico da função está localizado acima do eixo, É por isso:

Responder:

Quem tem dificuldades em calcular a integral definida e aplicar a fórmula de Newton-Leibniz , consulte a palestra Integral definida. Exemplos de soluções.

Exemplo 2

Calcule a área de uma figura delimitada por linhas, e eixo

Este é um exemplo para você resolver sozinho. Solução completa e resposta no final da lição.

O que fazer se o trapézio curvo estiver localizado embaixo do eixo?

Exemplo 3

Calcule a área da figura delimitada por linhas e eixos coordenados.

Solução: Vamos fazer um desenho:

Se um trapézio curvo completamente localizado sob o eixo, então sua área pode ser encontrada usando a fórmula:
Nesse caso:

Atenção! Os dois tipos de tarefas não devem ser confundidos:

1) Se lhe for solicitado que resolva simplesmente uma integral definida sem qualquer significado geométrico, então ela pode ser negativa.

Na prática, na maioria das vezes a figura está localizada no semiplano superior e inferior e, portanto, dos problemas escolares mais simples passamos para exemplos mais significativos.

Exemplo 4

Encontre a área de uma figura plana limitada pelas linhas , .

Solução: Primeiro você precisa fazer um desenho. De modo geral, ao construir um desenho em problemas de área, estamos mais interessados nos pontos de intersecção das retas. Vamos encontrar os pontos de intersecção da parábola e da reta. Isso pode ser feito de duas maneiras. O primeiro método é analítico. Resolvemos a equação:

Isso significa que o limite inferior de integração é, o limite superior de integração é.
É melhor não usar este método, se possível.

E agora a fórmula de trabalho: Se em um segmento existe alguma função contínua Melhor que ou igual a alguma função contínua, então a área da figura correspondente pode ser encontrada usando a fórmula:

No exemplo em consideração, é óbvio que no segmento a parábola está localizada acima da reta e, portanto, é necessário subtrair de

A solução completa pode ser assim:

A figura desejada é limitada por uma parábola acima e uma linha reta abaixo.
No segmento, de acordo com a fórmula correspondente:

Responder:

Na verdade, a fórmula escolar para a área de um trapézio curvilíneo no semiplano inferior (ver exemplo simples nº 3) é um caso especial da fórmula . Como o eixo é especificado pela equação e o gráfico da função está localizado abaixo do eixo, então

E agora alguns exemplos para sua própria solução

Exemplo 5

Exemplo 6

Encontre a área da figura delimitada pelas linhas , .

Exemplo 7

Calcule a área da figura delimitada pelas linhas , , , .

Primeiro vamos fazer um desenho:

A figura cuja área precisamos encontrar está sombreada em azul(observe atentamente a condição - como o número é limitado!). Mas na prática, por desatenção, muitas vezes surge a necessidade de encontrar a área de uma figura sombreada em verde!

Este exemplo também é útil porque calcula a área de uma figura usando duas integrais definidas. Realmente:

1) No segmento acima do eixo há um gráfico de uma reta;

2) No segmento acima do eixo está o gráfico de uma hipérbole.

É bastante óbvio que as áreas podem (e devem) ser somadas, portanto:

Responder:

Exemplo 8

Nesses casos, é necessário dedicar mais tempo e esclarecer analiticamente os limites da integração.

Vamos encontrar os pontos de intersecção de uma linha reta e uma parábola.
Para fazer isso, resolvemos a equação:

Por isso, .

A solução adicional é trivial, o principal é não se confundir com substituições e sinais; os cálculos aqui não são dos mais simples;

No segmento , de acordo com a fórmula correspondente:

Responder:

Bem, para concluir a lição, vejamos mais duas tarefas difíceis.

Exemplo 9

Calcule a área da figura delimitada pelas linhas , ,

Solução: Vamos representar esta figura no desenho.

Para construir um desenho ponto a ponto, você precisa conhecer a aparência de uma senóide (e em geral é útil saber gráficos de todas as funções elementares), bem como alguns valores de seno, eles podem ser encontrados em tabela trigonométrica. Em alguns casos (como neste caso), é possível construir um desenho esquemático, no qual os gráficos e limites de integração devem ser apresentados fundamentalmente de forma correta.

Não há problemas com os limites de integração aqui; eles decorrem diretamente da condição: - “x” muda de zero para “pi”. Vamos tomar outra decisão:

No segmento, o gráfico da função está localizado acima do eixo, portanto:

(1) Você pode ver como senos e cossenos são integrados em potências ímpares na lição Integrais de funções trigonométricas. Esta é uma técnica típica, arrancamos um seio.

(2) Usamos a identidade trigonométrica principal na forma

(3) Vamos mudar a variável, então:

Novas áreas de integração:

Quem é muito ruim com substituições, por favor, faça uma lição. Método de substituição em integral indefinida. Para quem não entende muito bem o algoritmo de substituição em integral definida, visite a página Integral definida. Exemplos de soluções.

Nº___ Data________

Assunto:Trapézio curvilíneo e sua área b

lições objetivas: Defina um trapézio curvo e sua área, aprenda a calcular a área de um trapézio curvo.

DURANTE AS AULAS

1. Momento organizacional.

Cumprimentar os alunos, verificando o preparo da turma para a aula, organizando a atenção dos alunos, revelando os objetivos gerais da aula e seu plano.

2. Etapa de verificação do dever de casa.

Objetivos: Estabelecer a correção, integralidade e consciência do desempenho dos trabalhos de casa por todos os alunos, para identificar lacunas no conhecimento e métodos de atividade dos alunos. Determine as causas das dificuldades e elimine as lacunas encontradas.

3. Estágio de atualização.

Objetivos: garantir a motivação da aprendizagem dos alunos, inclusão em atividades conjuntas para determinar os objetivos da aula. Atualizar a experiência subjetiva dos alunos.

Vamos lembrar os conceitos e fórmulas básicas.

Definição. Função e =f(x),x (a,b),é chamada de antiderivada da função y=f(x),x (a,b), se para todos x (a, b) igualdade vale

F (x)=f(x).

Comente. Se f(x) existe uma antiderivada para a função f(x), então para qualquer constante COM, F(x)+C também é uma antiderivada para f(x).

O problema de encontrar todas as antiderivadas de uma função f(x)é chamado de integração, e o conjunto de todas as antiderivadas é chamado de integral indefinida para a função f(x) Por dx e é designado

As seguintes propriedades ocorrem:

1 . ;

2 . Se C = Const, então
;

3 .
.

Comente. Nos cursos escolares de matemática, o termo “integral indefinida” não é usado; em vez disso, eles dizem “o conjunto de todas as antiderivadas”.

Aqui está uma tabela de integrais indefinidas.

Exemplo 1. Encontre uma antiderivada para uma função
, passando pelo ponto M(2;4).

Solução. O conjunto de todas as antiderivadas de uma função
existe uma integral indefinida
. Vamos calculá-lo usando as propriedades da integral 1 e 2. Nós temos:

Descobrimos que o conjunto de todas as antiderivadas é dado por uma família de funções y=F(x)+C, aquilo é y=x 3 – 2x+C, Onde COM– constante arbitrária.

Sabendo que a antiderivada passa pelo ponto M(2;4), substitua suas coordenadas na expressão anterior e encontre COM.

4=2 3 –2 2+COM  COM=4–8+4; COM=0.

Responder: F(x)=x 3 - 2x- a antiderivada desejada.

4. Formação de novos conceitos e métodos de atuação.

Objetivos: Garantir que os alunos percebam, compreendam e lembrem o material que está sendo estudado. Garantir que os alunos dominem os métodos de reprodução do material estudado, promovam a compreensão filosófica dos conceitos, leis, regras e fórmulas que estão sendo adquiridas. Estabelecer a correção e consciência do material estudado pelos alunos, identificar lacunas na compreensão primária e realizar correções. Certifique-se de que os alunos correlacionem sua experiência subjetiva com sinais de conhecimento científico.

Encontrando as áreas de figuras planas

O problema de encontrar a área de uma figura plana está intimamente relacionado ao problema de encontrar antiderivadas (integração). A saber: a área de um trapézio curvilíneo limitada pelo gráfico de uma funçãoy=f(x) (f(x)> 0) diretox=uma; x=b; e = 0, igual à diferença entre os valores da antiderivada da funçãoy=f(x) em pontosb Ea :

S=F(b)–F(a)

Vamos dar a definição de uma integral definida.

SOBRE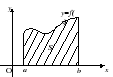
determinação. Deixe a função y=f(x) definido e integrável no intervalo [ um,b] deixa para lá F(x)- alguns de seus protótipos. Então o número F(b)–F(a) chamada de integral de A antes b funções f(x) e é designado

Igualdade
chamada de fórmula de Newton-Leibniz.

Esta fórmula conecta o problema de encontrar a área de uma figura plana com uma integral.

Em geral, se a figura for limitada por gráficos de funções y=f(x);y=g(x) (f(x)>g(x)) e liso x=uma;x=b, então sua área é igual a:

Exemplo 2. Em que ponto do gráfico da função y=x 2 + 1 você precisa desenhar uma tangente para que ela separe da figura formada pelo gráfico desta função e das retas e = 0,x = 0,x = 1 trapézio com a maior área?

Solução. Deixar M 0 (x 0 , sim 0 ) – ponto do gráfico da função y=x 2 + 1, em que a tangente necessária é desenhada.

Vamos encontrar a equação tangente s = s 0 +f (x 0 )(x-x 0 ) .

Nós temos:

É por isso

.

Encontre a área do trapézio OABC.

B– ponto de intersecção da tangente com a reta x = 1 

A tarefa foi reduzida a encontrar o maior valor da função

S(x)=–x 2 +x+ 1 no segmento. Nós vamos encontrar S (x)=– 2x+ 1. Encontre o ponto crítico da condição S (x)= 0  x =.

Vemos que a função atinge seu maior valor em x =. Nós vamos encontrar
.

Responder: a tangente deve ser traçada no ponto
.

Observe que o problema de encontrar uma integral com base em seu significado geométrico é frequentemente encontrado. Vamos mostrar com um exemplo como esse problema é resolvido.

Exemplo 4. Usando o significado geométrico da integral, calcule

A )
; b)
.

Solução.

A)
– igual à área de um trapézio curvilíneo delimitado por linhas.

P vamos transformar

– a metade superior do círculo com o centro R(1;0) e raio R = 1.

É por isso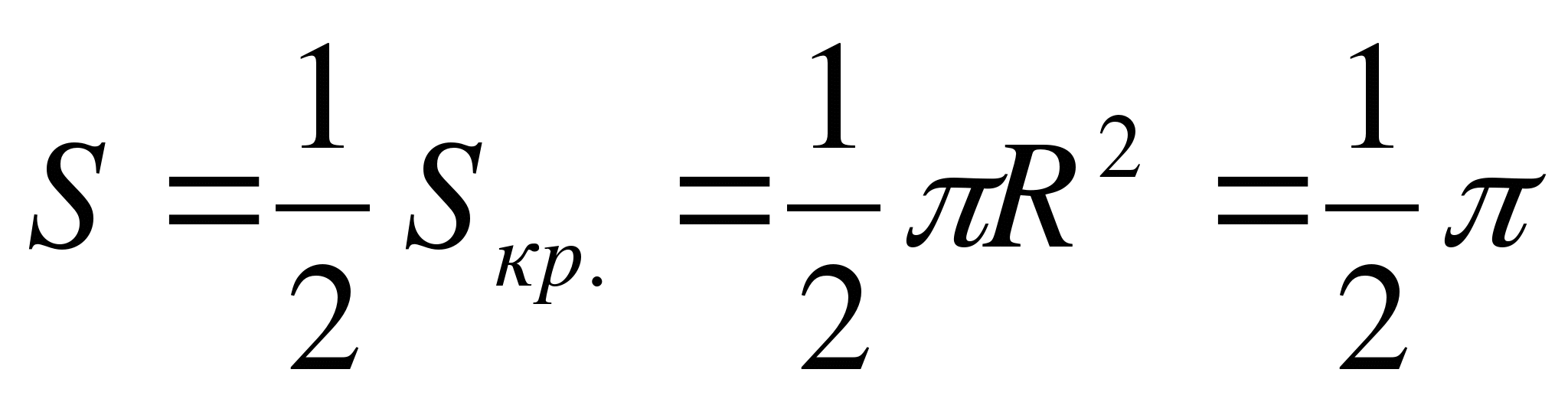
.

Responder:
.

b) Argumentando de forma semelhante, vamos construir uma área limitada por gráficos .2 – 2x+ 2, tangente a ele nos pontos A
, B(4;2)

e =–9x– 59, parábola e = 3x 2 +machado+ 1, se for conhecido que a tangente à parábola no ponto x=– 2 está com eixo Boi tamanho do ângulo arco 6.

Encontrar A, se for conhecido que a área de um trapézio curvilíneo delimitado por linhas e = 3x 3 + 2x, x=uma, y= 0 é igual a um.

Encontre a menor área de uma figura limitada por uma parábola y=x 2 + 2x– 3 e liso y=kx+ 1.

6. Estágio de informação do dever de casa.

Objetivos: Garantir que os alunos compreendam o propósito, o conteúdo e os métodos de realização dos trabalhos de casa nº 18, 19,20,21 ímpares.

7. Resumindo a lição.

Objetivo: Fornecer uma avaliação qualitativa do trabalho da turma e de cada aluno.

Exemplo 1 . Calcule a área da figura delimitada pelas linhas: x + 2y – 4 = 0, y = 0, x = -3 e x = 2

Vamos construir uma figura (ver figura) Construímos uma linha reta x + 2y – 4 = 0 usando dois pontos A(4;0) e B(0;2). Expressando y através de x, obtemos y = -0,5x + 2. Usando a fórmula (1), onde f(x) = -0,5x + 2, a = -3, b = 2, encontramos

S = = [-0,25=11,25 m². unidades

Exemplo 2. Calcule a área da figura delimitada pelas linhas: x – 2y + 4 = 0, x + y – 5 = 0 e y = 0.

Solução. Vamos construir a figura.

Vamos construir uma linha reta x – 2y + 4 = 0: y = 0, x = - 4, A(-4; 0); x = 0, y = 2, B(0; 2).

Vamos construir uma linha reta x + y – 5 = 0: y = 0, x = 5, C(5; 0), x = 0, y = 5, D(0; 5).

Vamos encontrar o ponto de intersecção das retas resolvendo o sistema de equações:

x = 2, y = 3; M(2;3).

Para calcular a área necessária, dividimos o triângulo AMC em dois triângulos AMN e NMC, pois quando x muda de A para N, a área é limitada por uma linha reta, e quando x muda de N para C - por uma linha reta

Para o triângulo AMN temos: ; y = 0,5x + 2, ou seja, f(x) = 0,5x + 2, a = - 4, b = 2.

Para o triângulo NMC temos: y = - x + 5, ou seja, f(x) = - x + 5, a = 2, b = 5.

Calculando a área de cada triângulo e somando os resultados, encontramos:

quadrado. unidades

9 + 4, 5 = 13,5 m². unidades Verifique: = 0,5AC = 0,5 sq. unidades

Exemplo 3. Calcule a área de uma figura delimitada por linhas: y = x 2 , y = 0, x = 2, x = 3.

Neste caso, você precisa calcular a área de um trapézio curvo limitado pela parábola y = x 2 , linhas retas x = 2 e x = 3 e o eixo do Boi (ver figura) Usando a fórmula (1) encontramos a área do trapézio curvilíneo

= = 6 m² unidades

Exemplo 4. Calcule a área da figura delimitada pelas linhas: y = - x 2 + 4 e y = 0

Vamos construir a figura. A área necessária está entre a parábola y = - x 2 + 4 e o eixo do Boi.

Vamos encontrar os pontos de intersecção da parábola com o eixo do Boi. Assumindo y = 0, encontramos x = Como esta figura é simétrica em relação ao eixo Oy, calculamos a área da figura localizada à direita do eixo Oy e dobramos o resultado obtido: = +4x]sq. unidades 2 = 2 m² unidades

Exemplo 5. Calcule a área de uma figura delimitada por linhas: y 2 = x, yx = 1, x = 4

Aqui você precisa calcular a área de um trapézio curvilíneo limitado pelo ramo superior da parábola 2 = x, eixo Boi e linhas retas x = 1 и x = 4 (ver figura)

De acordo com a fórmula (1), onde f(x) = a = 1 e b = 4, temos = (= unidades quadradas.

Exemplo 6 . Calcule a área da figura delimitada pelas linhas: y = sinx, y = 0, x = 0, x= .

A área necessária é limitada pela meia onda da senóide e pelo eixo Ox (ver figura).

Temos - cosx = - cos = 1 + 1 = 2 sq. unidades

Exemplo 7. Calcule a área da figura delimitada pelas linhas: y = - 6x, y = 0 e x = 4.

A figura está localizada sob o eixo do Boi (ver figura).

Portanto, encontramos sua área usando a fórmula (3)

= =

Exemplo 8. Calcule a área da figura delimitada pelas linhas: y = e x = 2. Construa a curva y = por pontos (ver figura). Assim, encontramos a área da figura usando a fórmula (4)

Exemplo 9 .

X 2 + você 2 = r 2 .

Aqui você precisa calcular a área delimitada pelo círculo x 2 + você 2 = r 2 , ou seja, a área de um círculo de raio r com centro na origem. Vamos encontrar a quarta parte desta área tomando os limites de integração de 0

antes; Nós temos: 1 = = [

Por isso, 1 =

Exemplo 10. Calcule a área de uma figura delimitada por linhas: y= x 2 e y = 2x

Esta figura é limitada pela parábola y = x 2 e a reta y = 2x (ver figura) Para determinar os pontos de intersecção das retas dadas, resolvemos o sistema de equações: x 2 – 2x = 0 x = 0 e x = 2

Usando a fórmula (5) para encontrar a área, obtemos

= \- -fl -- Г -1-±Л_ 1V1 -l-l-Ii-^ 3) |_ 2 3V 2 / J 3 24 24* Exemplo 2. Vamos calcular a área limitada pela senóide y = sinXy, o Boi eixo e a linha reta (Fig. .87). Aplicando a fórmula (I), obtemos A 2 S= J sinxdx= [-cos x]Q =0 -(-1) = lf Exemplo 3. Calcule a área limitada pelo arco da senóide ^у = sin jc, incluída entre dois pontos de intersecção adjacentes com o eixo do Boi (por exemplo, entre a origem e o ponto com a abcissa i). Observe que pelas considerações geométricas fica claro que esta área será o dobro da área do exemplo anterior. Porém, vamos fazer os cálculos: I 5= | s\nxdx= [ - cosх)* - - cos i-(-cos 0)= 1 + 1 = 2. o Na verdade, nossa suposição revelou-se correta. Exemplo 4. Calcule a área delimitada pela senóide e pelo eixo do Boi em um período (Fig. 88). Cálculos preliminares sugerem que a área será quatro vezes maior do que no Exemplo 2. Porém, após fazer os cálculos, obtemos “i Г,*i S - \ sin x dx = [ - cos x]0 = = - cos 2l -( -cos 0) = - 1 + 1 = 0. Este resultado requer esclarecimento. Para esclarecer a essência da questão, calculamos também a área limitada pela mesma senóide y = sin l: e o eixo do Boi na faixa de l a 2i. Aplicando a fórmula (I), obtemos 2l $2l sin xdx=[ - cosх]l = -cos 2i~)-c05i=- 1-1 =-2. Assim, vemos que esta área acabou por ser negativa. Comparando com a área calculada no exercício 3, descobrimos que seus valores absolutos são iguais, mas os sinais são diferentes. Se aplicarmos a propriedade V (ver Capítulo XI, § 4), obtemos 2l I 2l J sin xdx= J sin * dx [ sin x dx = 2 + (- 2) = 0O que aconteceu neste exemplo não é um acidente. Sempre a área localizada abaixo do eixo do Boi, desde que a variável independente mude da esquerda para a direita, é obtida quando calculada através de integrais. Neste curso consideraremos sempre áreas sem sinalização. Portanto, a resposta no exemplo que acabamos de discutir será: a área necessária é 2 + |-2| = 4. Exemplo 5. Vamos calcular a área do BAB mostrado na Fig. 89. Esta área é limitada pelo eixo do Boi, pela parábola y = - xr e pela reta y - = -x+\. Área de um trapézio curvilíneo A área necessária OAB consiste em duas partes: OAM e MAV. Como o ponto A é o ponto de intersecção de uma parábola e uma reta, encontraremos suas coordenadas resolvendo o sistema de equações 3 2 Y = mx. (precisamos apenas encontrar a abcissa do ponto A). Resolvendo o sistema, encontramos l; = ~. Portanto, a área deve ser calculada em partes, primeiro ao quadrado. OAM e depois pl. MAV: .... G 3 2, 3 G xP 3 1/2 U 2. QAM-^x)

Exemplos de área de trapézio curvo. Integral definida. Como calcular a área de uma figura. Estágio de informações sobre o dever de casa

Integral definida. Como calcular a área de uma figura

Artigos sobre o tema