เอ็กซ์ตรีมของฟังก์ชัน สุดขั้วของฟังก์ชัน ฟังก์ชันเพิ่มและลดฟังก์ชัน
ด้วยบริการนี้คุณสามารถทำได้ ค้นหาค่าที่ใหญ่ที่สุดและน้อยที่สุดของฟังก์ชันตัวแปรหนึ่งตัว f(x) พร้อมโซลูชันที่จัดรูปแบบใน Word ถ้ากำหนดฟังก์ชัน f(x,y) ไว้ ก็จำเป็นต้องค้นหาจุดสิ้นสุดของฟังก์ชันของตัวแปรสองตัว คุณยังสามารถค้นหาช่วงเวลาของฟังก์ชันเพิ่มและลดได้
กฎสำหรับการเข้าฟังก์ชั่น:
เงื่อนไขที่จำเป็นสำหรับฟังก์ชันสุดขั้วของตัวแปรหนึ่งตัว
สมการ f" 0 (x *) = 0 เป็นเงื่อนไขที่จำเป็นสำหรับปลายสุดของฟังก์ชันของตัวแปรตัวหนึ่ง นั่นคือ ณ จุด x * อนุพันธ์อันดับหนึ่งของฟังก์ชันจะต้องหายไป โดยระบุจุดที่คงที่ x c ซึ่งฟังก์ชันไม่อยู่ เพิ่มขึ้นหรือลดลงเงื่อนไขที่เพียงพอสำหรับปลายสุดของฟังก์ชันของตัวแปรหนึ่งตัว
ให้ f 0 (x) สามารถหาอนุพันธ์ได้สองเท่าโดยเทียบกับ x ที่อยู่ในเซต D หากตรงจุด x * ตรงตามเงื่อนไข:ฉ" 0 (x *) = 0
ฉ"" 0 (x *) > 0
จากนั้นจุด x * คือจุดต่ำสุดภายใน (ทั่วโลก) ของฟังก์ชัน
หากตรงจุด x * ตรงตามเงื่อนไข:
ฉ" 0 (x *) = 0
ฉ"" 0 (x *)< 0
จากนั้นจุด x * คือค่าสูงสุดเฉพาะที่ (ทั่วโลก)
ตัวอย่างหมายเลข 1 ค้นหาค่าที่ใหญ่ที่สุดและเล็กที่สุดของฟังก์ชัน: บนเซ็กเมนต์
สารละลาย. ![]()
จุดวิกฤติคือหนึ่ง x 1 = 2 (f’(x)=0) จุดนี้เป็นของกลุ่ม (จุด x=0 ไม่สำคัญ เนื่องจาก 0∉)
เราคำนวณค่าของฟังก์ชันที่ส่วนท้ายของส่วนและที่จุดวิกฤติ
ฉ(1)=9, ฉ(2)= 5 / 2 , ฉ(3)=3 8 / 81
คำตอบ: f นาที = 5/2 ที่ x=2; f สูงสุด =9 ที่ x=1
ตัวอย่างหมายเลข 2 ใช้อนุพันธ์ลำดับที่สูงกว่า หาจุดสิ้นสุดของฟังก์ชัน y=x-2sin(x)
สารละลาย.
ค้นหาอนุพันธ์ของฟังก์ชัน: y’=1-2cos(x) . มาหาจุดวิกฤตกันดีกว่า: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z เราพบว่า y''=2sin(x) คำนวณ ซึ่งหมายความว่า x= π / 3 +2πk, k∈Z คือจุดต่ำสุดของฟังก์ชัน ![]() ซึ่งหมายความว่า x=- π / 3 +2πk, k∈Z คือจุดสูงสุดของฟังก์ชัน
ซึ่งหมายความว่า x=- π / 3 +2πk, k∈Z คือจุดสูงสุดของฟังก์ชัน
ตัวอย่างหมายเลข 3 ตรวจสอบฟังก์ชันสุดขั้วในบริเวณใกล้กับจุด x=0
สารละลาย. ในที่นี้จำเป็นต้องค้นหาจุดสุดขีดของฟังก์ชัน หากค่าสุดขีด x=0 ให้ค้นหาประเภทของค่านั้น (ต่ำสุดหรือสูงสุด) หากจุดที่พบไม่มี x = 0 ให้คำนวณค่าของฟังก์ชัน f(x=0)
ควรสังเกตว่าเมื่ออนุพันธ์ในแต่ละด้านของจุดที่กำหนดไม่เปลี่ยนเครื่องหมาย สถานการณ์ที่เป็นไปได้จะไม่หมดลงแม้แต่ฟังก์ชันที่หาอนุพันธ์ได้: มันสามารถเกิดขึ้นได้สำหรับย่านใกล้เคียงขนาดเล็กโดยพลการที่ด้านหนึ่งของจุด x 0 หรือ ทั้งสองด้านมีเครื่องหมายการเปลี่ยนแปลงอนุพันธ์ ณ จุดเหล่านี้ จำเป็นต้องใช้วิธีอื่นเพื่อศึกษาฟังก์ชันในระดับสุดขั้ว
ตัวอย่างหมายเลข 4 แบ่งเลข 49 ออกเป็นสองพจน์ซึ่งผลคูณจะมากที่สุด
สารละลาย. ให้เราแสดงว่า x เป็นเทอมแรก จากนั้น (49-x) คือเทอมที่สอง
ผลิตภัณฑ์จะมีค่าสูงสุด: x·(49-x) → สูงสุด
หรือ
49x - x 2
ปริมาตรกระบอกสูบที่ใหญ่ที่สุด
ค้นหาขนาดของกระบอกสูบที่มีปริมาตรมากที่สุดซึ่งทำจากชิ้นงานที่มีรูปร่างคล้ายลูกบอลรัศมี Rสารละลาย:

ปริมาตรของทรงกระบอกคือ: V = πr 2 H
โดยที่ H = 2h
ลองแทนค่าเหล่านี้ลงในฟังก์ชันวัตถุประสงค์
วี → สูงสุด
ลองหาปลายสุดของฟังก์ชันกัน เนื่องจากฟังก์ชันปริมาตร V(h) ขึ้นอยู่กับตัวแปรเพียงตัวเดียว เราจะค้นหาอนุพันธ์โดยใช้บริการนี้
จากบทความนี้ ผู้อ่านจะได้เรียนรู้เกี่ยวกับคุณค่าการทำงานขั้นสูงสุด รวมถึงคุณสมบัติของการใช้งานในกิจกรรมภาคปฏิบัติ การศึกษาแนวคิดดังกล่าวมีความสำคัญอย่างยิ่งในการทำความเข้าใจรากฐานของคณิตศาสตร์ระดับสูง หัวข้อนี้เป็นหัวข้อพื้นฐานสำหรับการศึกษาเชิงลึกของหลักสูตร
ติดต่อกับ
สุดขั้วคืออะไร?
ในหลักสูตรของโรงเรียน มีการให้คำจำกัดความมากมายของแนวคิด "สุดขั้ว" บทความนี้มีวัตถุประสงค์เพื่อให้ความเข้าใจที่ลึกซึ้งและชัดเจนที่สุดเกี่ยวกับคำศัพท์สำหรับผู้ที่ไม่รู้ประเด็น ดังนั้นจึงเข้าใจได้ว่าช่วงการทำงานจะได้ค่าต่ำสุดหรือสูงสุดในชุดใดชุดหนึ่ง
สุดขีดคือทั้งค่าต่ำสุดของฟังก์ชันและค่าสูงสุดในเวลาเดียวกัน มีจุดต่ำสุดและจุดสูงสุดนั่นคือค่าสุดขีดของอาร์กิวเมนต์บนกราฟ ศาสตร์หลักที่ใช้แนวคิดนี้คือ:
- สถิติ;
- การควบคุมเครื่องจักร
- เศรษฐมิติ
จุดสุดโต่งมีบทบาทสำคัญในการกำหนดลำดับของฟังก์ชันที่กำหนด ระบบพิกัดในกราฟที่ดีที่สุดจะแสดงการเปลี่ยนแปลงในตำแหน่งสุดขั้วโดยขึ้นอยู่กับการเปลี่ยนแปลงฟังก์ชันการทำงาน
สุดขีดของฟังก์ชันอนุพันธ์
นอกจากนี้ยังมีปรากฏการณ์เช่น "อนุพันธ์" มีความจำเป็นต้องกำหนดจุดปลายสุด สิ่งสำคัญคืออย่าสับสนระหว่างคะแนนต่ำสุดหรือสูงสุดกับค่าสูงสุดและต่ำสุด สิ่งเหล่านี้เป็นแนวคิดที่แตกต่างกัน แม้ว่าอาจดูคล้ายกันก็ตาม
ค่าของฟังก์ชันเป็นปัจจัยหลักในการกำหนดวิธีหาจุดสูงสุด อนุพันธ์ไม่ได้ถูกสร้างขึ้นจากค่านิยม แต่มาจากตำแหน่งสุดขั้วในลำดับใดลำดับหนึ่งเท่านั้น
อนุพันธ์นั้นพิจารณาจากจุดสุดขั้วเหล่านี้ และไม่ใช่จากมูลค่าที่ใหญ่ที่สุดหรือน้อยที่สุด ในโรงเรียนของรัสเซีย เส้นแบ่งระหว่างแนวคิดทั้งสองนี้ไม่ได้วาดไว้อย่างชัดเจน ซึ่งส่งผลต่อความเข้าใจในหัวข้อนี้โดยทั่วไป
ตอนนี้ให้เราพิจารณาแนวคิดเช่น "ภาวะสุดโต่งเฉียบพลัน" วันนี้มีค่าต่ำสุดเฉียบพลันและค่าสูงสุดเฉียบพลัน คำจำกัดความได้รับตามการจำแนกจุดวิกฤตของฟังก์ชันของรัสเซีย แนวคิดเรื่องจุดสุดขั้วเป็นพื้นฐานในการค้นหาจุดวิกฤตบนกราฟ

เพื่อกำหนดแนวคิดดังกล่าว พวกเขาใช้ทฤษฎีบทของแฟร์มาต์ มันเป็นสิ่งสำคัญที่สุดในการศึกษาจุดสุดขั้วและให้ความคิดที่ชัดเจนเกี่ยวกับการมีอยู่ของมันในรูปแบบใดรูปแบบหนึ่ง เพื่อให้มั่นใจถึงความสุดขั้ว สิ่งสำคัญคือต้องสร้างเงื่อนไขบางประการสำหรับการลดลงหรือเพิ่มขึ้นบนกราฟ
หากต้องการตอบคำถาม “วิธีหาจุดสูงสุด” อย่างถูกต้อง คุณต้องปฏิบัติตามหลักเกณฑ์เหล่านี้:
- การค้นหาโดเมนคำจำกัดความที่แน่นอนบนกราฟ
- ค้นหาอนุพันธ์ของฟังก์ชันและจุดปลายสุด
- แก้ความไม่เท่าเทียมกันมาตรฐานสำหรับโดเมนที่พบอาร์กิวเมนต์
- สามารถพิสูจน์ได้ว่าฟังก์ชันใดที่จุดบนกราฟถูกกำหนดและต่อเนื่องกัน

ความสนใจ!การค้นหาจุดวิกฤติของฟังก์ชันจะเป็นไปได้ก็ต่อเมื่อมีอนุพันธ์ในลำดับที่สองเป็นอย่างน้อย ซึ่งมั่นใจได้จากสัดส่วนที่สูงของการมีอยู่ของจุดสุดขั้ว
เงื่อนไขที่จำเป็นสำหรับส่วนปลายของฟังก์ชัน
เพื่อให้สุดขั้วมีอยู่ สิ่งสำคัญคือต้องมีทั้งจุดต่ำสุดและสูงสุด หากปฏิบัติตามกฎนี้เพียงบางส่วนเท่านั้น เงื่อนไขของการมีอยู่ของสุดขั้วจะถูกละเมิด

แต่ละฟังก์ชันในตำแหน่งใดๆ จะต้องมีความแตกต่างกันเพื่อให้สามารถระบุความหมายใหม่ได้ สิ่งสำคัญคือต้องเข้าใจว่ากรณีที่จุดที่กลายเป็นศูนย์ไม่ใช่หลักการหลักในการค้นหาจุดที่หาอนุพันธ์ได้
ค่าสุดโต่งเฉียบพลันและฟังก์ชันขั้นต่ำเป็นส่วนสำคัญอย่างยิ่งในการแก้ปัญหาทางคณิตศาสตร์โดยใช้ค่าสุดขั้ว เพื่อให้เข้าใจส่วนประกอบนี้ได้ดีขึ้น สิ่งสำคัญคือต้องอ้างอิงค่าแบบตารางเพื่อระบุฟังก์ชันการทำงาน
| การวิจัยความหมายเต็มรูปแบบ | พล็อตกราฟค่า |
| 1. การกำหนดจุดเพิ่มและลดค่า 2. การหาจุดไม่ต่อเนื่อง ปลายสุด และจุดตัดด้วยแกนพิกัด 3. กระบวนการพิจารณาการเปลี่ยนแปลงตำแหน่งบนกราฟ 4. การกำหนดตัวบ่งชี้และทิศทางของความนูนและความนูนโดยคำนึงถึงการมีอยู่ของเส้นกำกับ 5. การสร้างตารางสรุปการวิจัยจากมุมมองของการกำหนดพิกัด 6. การหาช่วงเวลาของการเพิ่มขึ้นและลดลงของจุดสุดขั้วและจุดแหลมคม 7. การหาค่าความนูนและความเว้าของเส้นโค้ง 8. การวาดกราฟโดยคำนึงถึงการวิจัยช่วยให้คุณค้นหาค่าต่ำสุดหรือสูงสุดได้ |
องค์ประกอบหลักเมื่อจำเป็นต้องทำงานกับจุดสุดขั้วคือการสร้างกราฟที่แม่นยำ ครูในโรงเรียนมักไม่ค่อยให้ความสำคัญกับประเด็นสำคัญดังกล่าวซึ่งเป็นการละเมิดกระบวนการศึกษาอย่างร้ายแรง การสร้างกราฟเกิดขึ้นจากผลการศึกษาข้อมูลเชิงฟังก์ชัน การระบุภาวะสุดขีดเฉียบพลัน และจุดบนกราฟเท่านั้น Sharp extrema ของฟังก์ชันอนุพันธ์จะแสดงบนพล็อตของค่าที่แน่นอน โดยใช้ขั้นตอนมาตรฐานในการกำหนดเส้นกำกับ จุดสูงสุดและต่ำสุดของฟังก์ชันจะมาพร้อมกับโครงสร้างกราฟที่ซับซ้อนยิ่งขึ้น นี่เป็นเพราะความต้องการที่ลึกซึ้งยิ่งขึ้นในการแก้ไขปัญหาภาวะหัวรุนแรงเฉียบพลัน นอกจากนี้ยังจำเป็นต้องค้นหาอนุพันธ์ของฟังก์ชันที่ซับซ้อนและเรียบง่าย เนื่องจากนี่เป็นหนึ่งในแนวคิดที่สำคัญที่สุดในปัญหาสุดขั้ว |
สุดขั้วของการทำงาน
หากต้องการค้นหาค่าข้างต้น คุณต้องปฏิบัติตามกฎต่อไปนี้:
- กำหนดเงื่อนไขที่จำเป็นสำหรับความสัมพันธ์ที่รุนแรง
- คำนึงถึงสภาพที่เพียงพอของจุดสุดขั้วบนกราฟ
- ดำเนินการคำนวณภาวะสุดขั้วเฉียบพลัน
แนวคิดเช่นค่าต่ำสุดที่อ่อนแอและค่าต่ำสุดที่แข็งแกร่งก็ถูกนำมาใช้เช่นกัน สิ่งนี้จะต้องนำมาพิจารณาเมื่อพิจารณาถึงจุดสุดยอดและการคำนวณที่แม่นยำ ในขณะเดียวกันฟังก์ชันการทำงานแบบเฉียบพลันคือการค้นหาและสร้างเงื่อนไขที่จำเป็นทั้งหมดสำหรับการทำงานกับกราฟของฟังก์ชัน
นี่เป็นส่วนที่ค่อนข้างน่าสนใจของคณิตศาสตร์ซึ่งผู้สำเร็จการศึกษาและนักศึกษาทุกคนต้องเผชิญ อย่างไรก็ตามไม่ใช่ทุกคนจะชอบมาทัน บางคนไม่สามารถเข้าใจสิ่งพื้นฐานได้ เช่น การศึกษาฟังก์ชันที่ดูเหมือนเป็นมาตรฐาน บทความนี้มีวัตถุประสงค์เพื่อแก้ไขการกำกับดูแลดังกล่าว ต้องการเรียนรู้เพิ่มเติมเกี่ยวกับการวิเคราะห์ฟังก์ชันหรือไม่ คุณต้องการทราบว่าจุดสุดขั้วคืออะไรและจะค้นหาได้อย่างไร บทความนี้เหมาะสำหรับคุณ
การศึกษากราฟของฟังก์ชัน
อันดับแรก ควรทำความเข้าใจว่าทำไมคุณจึงต้องวิเคราะห์กราฟเลย มีฟังก์ชั่นง่ายๆที่วาดได้ไม่ยาก ตัวอย่างที่ชัดเจนของฟังก์ชันดังกล่าวคือพาราโบลา การวาดกราฟไม่ใช่เรื่องยาก สิ่งที่คุณต้องมีคือใช้การแปลงแบบง่ายๆ เพื่อค้นหาตัวเลขที่ฟังก์ชันรับค่า 0 และโดยหลักการแล้ว นี่คือทั้งหมดที่คุณต้องรู้เพื่อวาดกราฟของพาราโบลา
แต่จะเกิดอะไรขึ้นถ้าฟังก์ชันที่เราต้องการสร้างกราฟนั้นซับซ้อนกว่านี้มาก? เนื่องจากคุณสมบัติของฟังก์ชันที่ซับซ้อนไม่ชัดเจนนัก จึงจำเป็นต้องทำการวิเคราะห์ทั้งหมด หลังจากนี้เท่านั้นจึงจะสามารถแสดงฟังก์ชันเป็นภาพกราฟิกได้ วิธีการทำเช่นนี้? คุณสามารถหาคำตอบสำหรับคำถามนี้ได้ในบทความนี้
แผนการวิเคราะห์ฟังก์ชัน
สิ่งแรกที่เราต้องทำคือทำการศึกษาฟังก์ชันแบบผิวเผิน ในระหว่างนั้นเราจะค้นหาโดเมนของคำจำกัดความ เรามาเริ่มกันตามลำดับ โดเมนของคำจำกัดความคือชุดของค่าที่ฟังก์ชันถูกกำหนดไว้ พูดง่ายๆ ก็คือตัวเลขเหล่านี้สามารถนำมาใช้ในฟังก์ชันแทน x ได้ ในการกำหนดขอบเขต คุณเพียงแค่ต้องดูที่บันทึก ตัวอย่างเช่น เห็นได้ชัดว่าฟังก์ชัน y (x) = x 3 + x 2 - x + 43 มีโดเมนของคำจำกัดความที่เป็นเซตของจำนวนจริง ด้วยฟังก์ชันเช่น (x 2 - 2x)/x ทุกอย่างแตกต่างออกไปเล็กน้อย เนื่องจากตัวเลขในตัวส่วนต้องไม่เท่ากับ 0 โดเมนของคำจำกัดความของฟังก์ชันนี้จะเป็นจำนวนจริงทั้งหมดที่ไม่ใช่ศูนย์
ต่อไปคุณจะต้องค้นหาสิ่งที่เรียกว่าศูนย์ของฟังก์ชัน นี่คือค่าอาร์กิวเมนต์ที่ฟังก์ชันทั้งหมดรับค่าเป็นศูนย์ ในการทำเช่นนี้จำเป็นต้องจัดฟังก์ชันให้เป็นศูนย์พิจารณาอย่างละเอียดและทำการแปลงบางอย่าง ลองใช้ฟังก์ชันที่คุ้นเคยอยู่แล้ว y(x) = (x 2 - 2x)/x จากหลักสูตรของโรงเรียน เรารู้ว่าเศษส่วนเท่ากับ 0 เมื่อตัวเศษเท่ากับศูนย์ ดังนั้นเราจึงละทิ้งตัวส่วนและเริ่มทำงานกับตัวเศษโดยทำให้มันเป็นศูนย์ เราได้ x 2 - 2x = 0 และนำ x ออกจากวงเล็บ ดังนั้น x (x - 2) = 0 ผลลัพธ์คือ เราพบว่าฟังก์ชันของเราเท่ากับศูนย์ เมื่อ x เท่ากับ 0 หรือ 2
เมื่อตรวจสอบกราฟของฟังก์ชัน หลายคนประสบปัญหาในรูปแบบของจุดสุดขั้ว และมันก็แปลก ท้ายที่สุดแล้ว ความสุดขั้วเป็นหัวข้อที่ค่อนข้างง่าย ไม่เชื่อฉันเหรอ? ดูตัวคุณเองโดยอ่านบทความนี้ซึ่งเราจะพูดถึงคะแนนต่ำสุดและสูงสุด

ประการแรก ควรทำความเข้าใจก่อนว่าภาวะสุดโต่งคืออะไร สุดขีดคือค่าขีดจำกัดที่ฟังก์ชันไปถึงบนกราฟ ปรากฎว่ามีค่าสูงสุดสองค่า - สูงสุดและต่ำสุด เพื่อความชัดเจนคุณสามารถดูภาพด้านบนได้ ในพื้นที่ศึกษา จุด -1 คือค่าสูงสุดของฟังก์ชัน y (x) = x 5 - 5x และจุดที่ 1 ตามลำดับคือค่าต่ำสุด
นอกจากนี้อย่าสับสนแนวคิด จุดปลายสุดของฟังก์ชันคืออาร์กิวเมนต์ที่ฟังก์ชันที่กำหนดได้รับค่าที่มากสุด ในทางกลับกัน ค่าสุดขีดคือค่าของค่าต่ำสุดและค่าสูงสุดของฟังก์ชัน ตัวอย่างเช่น ลองพิจารณาภาพด้านบนอีกครั้ง -1 และ 1 คือจุดสุดขีดของฟังก์ชัน และ 4 และ -4 คือจุดสุดขีดนั่นเอง
การหาจุดสุดยอด

แต่คุณจะหาจุดปลายสุดของฟังก์ชันได้อย่างไร? ทุกอย่างค่อนข้างง่าย สิ่งแรกที่ต้องทำคือหาอนุพันธ์ของสมการ สมมติว่าเราได้รับงาน: “ ค้นหาจุดปลายสุดของฟังก์ชัน y (x) x คืออาร์กิวเมนต์ เพื่อความชัดเจน ลองใช้ฟังก์ชัน y (x) = x 3 + 2x 2 + x + 54 มาแยกความแตกต่างและ จะได้สมการต่อไปนี้: 3x 2 + 4x + 1 ผลลัพธ์ที่ได้คือสมการกำลังสองมาตรฐาน สิ่งที่เราต้องทำต่อไปคือทำให้มันกลายเป็นศูนย์แล้วหาราก เนื่องจากค่าจำแนกมีค่ามากกว่าศูนย์ (D = 16 - 12 = 4) สมการนี้ถูกกำหนดโดยราก 2 ราก ค้นหาแล้วได้ค่า 2 ค่า: 1/3 และ -1 จุดเหล่านี้จะเป็นจุดปลายสุดของฟังก์ชัน อย่างไรก็ตาม คุณจะยังระบุได้อย่างไรว่าใครเป็นใคร จุดใดคือจุดสูงสุดและจุดใดคือจุดต่ำสุด ในการทำเช่นนี้ คุณต้องหาจุดใกล้เคียงและค้นหาค่าของมัน ตัวอย่างเช่น ใช้หมายเลข -2 ซึ่งอยู่ทางซ้ายตามแนวพิกัดจาก -1 . แทนค่านี้ลงในสมการของเรา y(-2) = 12 - 8 + 1 = 5. ผลลัพธ์ที่ได้คือจำนวนบวก ซึ่งหมายความว่า ในช่วงจาก ฟังก์ชันจะเพิ่มขึ้นจาก 1/3 เป็น -1 นี่ ในทางกลับกัน หมายความว่าในช่วงเวลาจากลบอนันต์ถึง 1/3 และจาก -1 ถึงบวกอนันต์ ฟังก์ชันจะลดลง ดังนั้น เราสามารถสรุปได้ว่าตัวเลข 1/3 คือจุดต่ำสุดของฟังก์ชันในช่วงเวลาที่ศึกษา และ -1 คือจุดสูงสุด

นอกจากนี้ยังเป็นที่น่าสังเกตว่าการสอบ Unified State ไม่เพียงต้องการการค้นหาจุดสุดขั้วเท่านั้น แต่ยังต้องดำเนินการบางอย่างด้วย (การบวกการคูณ ฯลฯ ) ด้วยเหตุนี้จึงควรให้ความสนใจเป็นพิเศษกับเงื่อนไขของปัญหา ท้ายที่สุดเนื่องจากการไม่ตั้งใจคุณอาจเสียคะแนนได้
จุดปลายสุดของฟังก์ชันคือจุดในโดเมนของคำจำกัดความของฟังก์ชันซึ่งค่าของฟังก์ชันเป็นค่าต่ำสุดหรือสูงสุด ค่าของฟังก์ชันที่จุดเหล่านี้เรียกว่า extrema (ต่ำสุดและสูงสุด) ของฟังก์ชัน.
คำนิยาม. จุด x1 โดเมนฟังก์ชัน ฉ(x) ถูกเรียก จุดสูงสุดของฟังก์ชัน หากค่าของฟังก์ชัน ณ จุดนี้มากกว่าค่าของฟังก์ชัน ณ จุดที่ใกล้กับมันเพียงพอซึ่งอยู่ทางขวาและซ้าย (นั่นคือ อสมการคงอยู่) ฉ(x0 ) > ฉ(x 0 + Δ x) x1 ขีดสุด.
คำนิยาม. จุด x2 โดเมนฟังก์ชัน ฉ(x) ถูกเรียก จุดต่ำสุดของฟังก์ชันหากค่าของฟังก์ชัน ณ จุดนี้น้อยกว่าค่าของฟังก์ชัน ณ จุดที่ใกล้กับมันเพียงพอซึ่งอยู่ทางขวาและซ้าย (นั่นคือ ความไม่เท่าเทียมกันยังคงอยู่ ฉ(x0 ) < ฉ(x 0 + Δ x) ). ในกรณีนี้เราบอกว่าฟังก์ชันมีตรงประเด็น x2 ขั้นต่ำ
สมมุติว่าจุด x1 - จุดสูงสุดของฟังก์ชัน ฉ(x) . จากนั้นในช่วงเวลาจนถึง x1 ฟังก์ชั่นเพิ่มขึ้นดังนั้นอนุพันธ์ของฟังก์ชันจึงมากกว่าศูนย์ ( ฉ "(x) > 0 ) และในช่วงเวลาหลังจากนั้น x1 ฟังก์ชั่นลดลง ดังนั้น อนุพันธ์ของฟังก์ชันน้อยกว่าศูนย์ ( ฉ "(x) < 0 ). Тогда в точке x1
ให้เราถือว่าประเด็นนั้นด้วย x2 - จุดต่ำสุดของฟังก์ชัน ฉ(x) . จากนั้นในช่วงเวลาจนถึง x2 ฟังก์ชันกำลังลดลง และอนุพันธ์ของฟังก์ชันมีค่าน้อยกว่าศูนย์ ( ฉ "(x) < 0 ), а в интервале после x2 ฟังก์ชันกำลังเพิ่มขึ้น และอนุพันธ์ของฟังก์ชันมีค่ามากกว่าศูนย์ ( ฉ "(x) > 0 ) ในกรณีนี้ก็ตรงประเด็นเช่นกัน x2 อนุพันธ์ของฟังก์ชันเป็นศูนย์หรือไม่มีอยู่จริง
ทฤษฎีบทของแฟร์มาต์ (สัญญาณที่จำเป็นของการมีอยู่ของฟังก์ชันสุดขั้ว). ถ้าตรงประเด็น x0 - จุดปลายสุดของฟังก์ชัน ฉ(x) จากนั้น ณ จุดนี้อนุพันธ์ของฟังก์ชันจะเท่ากับศูนย์ ( ฉ "(x) = 0 ) หรือไม่มีอยู่
คำนิยาม. จุดที่อนุพันธ์ของฟังก์ชันเป็นศูนย์หรือไม่มีอยู่เรียกว่า จุดวิกฤติ .

ตัวอย่างที่ 1ลองพิจารณาฟังก์ชันดู
ตรงจุด x= 0 อนุพันธ์ของฟังก์ชันเป็นศูนย์ ดังนั้นจุด x= 0 คือจุดวิกฤต อย่างไรก็ตาม ดังที่เห็นบนกราฟของฟังก์ชัน มันจะเพิ่มขึ้นตลอดขอบเขตคำจำกัดความ ดังนั้นจุด x= 0 ไม่ใช่จุดสิ้นสุดของฟังก์ชันนี้
ดังนั้น เงื่อนไขที่ว่าอนุพันธ์ของฟังก์ชันที่จุดหนึ่งเท่ากับศูนย์หรือไม่มีอยู่ จึงเป็นเงื่อนไขที่จำเป็นสำหรับจุดสุดโต่ง แต่ไม่เพียงพอ เนื่องจากสามารถให้ตัวอย่างฟังก์ชันอื่นๆ ที่ตรงตามเงื่อนไขเหล่านี้ได้ แต่ฟังก์ชัน ไม่มีปลายสุดที่จุดที่สอดคล้องกัน นั่นเป็นเหตุผล จะต้องมีหลักฐานเพียงพอช่วยให้สามารถตัดสินได้ว่ามีจุดสุดยอดที่จุดวิกฤติเฉพาะหรือไม่และจุดสุดยอดประเภทใด - สูงสุดหรือต่ำสุด
ทฤษฎีบท (สัญญาณแรกเพียงพอของการมีอยู่ของฟังก์ชันสุดขั้ว)จุดวิกฤติ x0 ฉ(x) หากเมื่อผ่านจุดนี้อนุพันธ์ของฟังก์ชันจะเปลี่ยนเครื่องหมายและหากเครื่องหมายเปลี่ยนจาก "บวก" เป็น "ลบ" แสดงว่าเป็นจุดสูงสุดและหากจาก "ลบ" เป็น "บวก" ดังนั้น มันเป็นจุดต่ำสุด
ถ้าอยู่ใกล้จุด x0 ไปทางซ้ายและขวาอนุพันธ์ยังคงมีเครื่องหมายซึ่งหมายความว่าฟังก์ชันจะลดลงหรือเพิ่มขึ้นเฉพาะในบริเวณใกล้เคียงของจุดเท่านั้น x0 . ในกรณีนี้ ณ จุดนั้น x0 ไม่มีความสุดขั้ว
ดังนั้น, เพื่อกำหนดจุดปลายสุดของฟังก์ชัน คุณต้องดำเนินการดังต่อไปนี้ :
- ค้นหาอนุพันธ์ของฟังก์ชัน
- เทียบอนุพันธ์ให้เป็นศูนย์แล้วหาจุดวิกฤต
- ทำเครื่องหมายจุดวิกฤติบนเส้นจำนวนทั้งทางจิตใจหรือบนกระดาษและกำหนดสัญญาณของอนุพันธ์ของฟังก์ชันในช่วงเวลาผลลัพธ์ หากเครื่องหมายของอนุพันธ์เปลี่ยนจาก "บวก" เป็น "ลบ" จุดวิกฤตคือจุดสูงสุด และหากจาก "ลบ" เป็น "บวก" ก็จะเป็นจุดต่ำสุด
- คำนวณค่าของฟังก์ชันที่จุดปลายสุด

ตัวอย่างที่ 2ค้นหาจุดสุดขีดของฟังก์ชัน ![]() .
.
สารละลาย. มาหาอนุพันธ์ของฟังก์ชันกัน:
ลองเทียบอนุพันธ์ให้เป็นศูนย์เพื่อค้นหาจุดวิกฤติ:
![]() .
.
เนื่องจากค่าใด ๆ ของ "x" ตัวส่วนไม่เท่ากับศูนย์เราจึงถือว่าตัวเศษเป็นศูนย์:
มีจุดวิกฤติหนึ่งจุด x= 3 . ให้เรากำหนดเครื่องหมายของอนุพันธ์ในช่วงเวลาที่คั่นด้วยจุดนี้:
ในช่วงตั้งแต่ลบอนันต์ถึง 3 - เครื่องหมายลบนั่นคือฟังก์ชันลดลง
ในช่วงตั้งแต่ 3 ถึงบวกอนันต์จะมีเครื่องหมายบวกนั่นคือฟังก์ชันเพิ่มขึ้น
นั่นก็คือช่วงเวลา x= 3 คือจุดต่ำสุด
มาหาค่าของฟังก์ชันที่จุดต่ำสุด:
ดังนั้นจึงพบจุดปลายสุดของฟังก์ชัน: (3; 0) และเป็นจุดต่ำสุด
ทฤษฎีบท (สัญญาณเพียงพอที่สองของการมีอยู่ของส่วนปลายของฟังก์ชัน)จุดวิกฤติ x0 คือจุดปลายสุดของฟังก์ชัน ฉ(x) ถ้าอนุพันธ์อันดับสองของฟังก์ชัน ณ จุดนี้ไม่เท่ากับศูนย์ ( ฉ ""(x) ≠ 0 ) และถ้าอนุพันธ์อันดับสองมากกว่าศูนย์ ( ฉ ""(x) > 0 ) แล้วจึงเป็นจุดสูงสุด และหากอนุพันธ์อันดับสองน้อยกว่าศูนย์ ( ฉ ""(x) < 0 ), то точкой минимума.
หมายเหตุ 1. ถ้าตรงจุด x0 ถ้าทั้งอนุพันธ์ตัวแรกและตัวที่สองหายไป เมื่อถึงจุดนี้ ก็เป็นไปไม่ได้ที่จะตัดสินการมีอยู่ของค่าสุดโต่งตามเกณฑ์ที่สองที่เพียงพอ ในกรณีนี้ คุณต้องใช้เกณฑ์แรกที่เพียงพอสำหรับส่วนปลายสุดของฟังก์ชัน
หมายเหตุ 2 เกณฑ์ที่สองที่เพียงพอสำหรับส่วนปลายของฟังก์ชันนั้นใช้ไม่ได้แม้ว่าอนุพันธ์อันดับ 1 จะไม่อยู่ที่จุดคงที่ก็ตาม (ดังนั้นอนุพันธ์อันดับ 2 ก็ไม่มีเช่นกัน) ในกรณีนี้ คุณจะต้องใช้เครื่องหมายที่เพียงพอตัวแรกของส่วนปลายของฟังก์ชันด้วย
ลักษณะเฉพาะของส่วนปลายสุดของฟังก์ชัน
จากคำจำกัดความข้างต้น พบว่าส่วนปลายสุดของฟังก์ชันมีลักษณะเฉพาะที่ ซึ่งเป็นค่าที่ใหญ่ที่สุดและน้อยที่สุดของฟังก์ชันเมื่อเปรียบเทียบกับค่าใกล้เคียง
สมมติว่าคุณกำลังดูรายได้ของคุณในช่วงระยะเวลาหนึ่งปี หากในเดือนพฤษภาคม คุณมีรายได้ 45,000 รูเบิล และในเดือนเมษายน 42,000 รูเบิล และในเดือนมิถุนายน 39,000 รูเบิล รายได้ในเดือนพฤษภาคมจะเป็นจำนวนสูงสุดของฟังก์ชันรายได้เมื่อเปรียบเทียบกับมูลค่าใกล้เคียง แต่ในเดือนตุลาคม คุณได้รับ 71,000 รูเบิล ในเดือนกันยายน 75,000 รูเบิล และในเดือนพฤศจิกายน 74,000 รูเบิล ดังนั้นรายได้ในเดือนตุลาคมจึงเป็นฟังก์ชันรายได้ขั้นต่ำเมื่อเทียบกับมูลค่าใกล้เคียง และคุณจะเห็นได้ง่ายๆ ว่าค่าสูงสุดระหว่างเดือนเมษายน-พฤษภาคม-มิถุนายนนั้นน้อยกว่าค่าต่ำสุดของเดือนกันยายน-ตุลาคม-พฤศจิกายน
โดยทั่วไปแล้ว ในช่วงเวลาหนึ่ง ฟังก์ชันอาจมีจุดสุดโต่งหลายจุด และอาจปรากฏว่าฟังก์ชันขั้นต่ำบางค่ามากกว่าค่าสูงสุดใดๆ ดังนั้น สำหรับฟังก์ชันที่แสดงในภาพด้านบน .
นั่นคือเราไม่ควรคิดว่าค่าสูงสุดและต่ำสุดของฟังก์ชันคือค่าที่ใหญ่ที่สุดและเล็กที่สุดในกลุ่มทั้งหมดที่อยู่ระหว่างการพิจารณาตามลำดับ ที่จุดสูงสุดฟังก์ชันจะมีค่ามากที่สุดเมื่อเปรียบเทียบกับค่าเหล่านั้นที่มี ณ จุดทั้งหมดใกล้กับจุดสูงสุดอย่างเพียงพอเท่านั้น และที่จุดต่ำสุดก็มีค่าน้อยที่สุดเมื่อเปรียบเทียบกับค่าเหล่านั้นเท่านั้น ว่ามีทุกจุดใกล้กับจุดต่ำสุดเพียงพอแล้ว
ดังนั้นเราจึงสามารถอธิบายแนวคิดข้างต้นเกี่ยวกับจุดปลายสุดของฟังก์ชันและเรียกจุดต่ำสุด จุดต่ำสุดในพื้นที่ และจุดสูงสุดในพื้นที่
เรามองหาส่วนปลายของฟังก์ชันด้วยกัน

ตัวอย่างที่ 3
วิธีแก้ไข: ฟังก์ชันถูกกำหนดและต่อเนื่องกันบนเส้นจำนวนทั้งหมด อนุพันธ์ของมัน ![]() มีอยู่บนเส้นจำนวนทั้งหมดด้วย ดังนั้นในกรณีนี้ จุดวิกฤตจึงเป็นเพียงจุดที่สำคัญเท่านั้น เช่น จากที่ไหน และ . จุดวิกฤติและแบ่งโดเมนทั้งหมดของคำจำกัดความของฟังก์ชันออกเป็นสามช่วงของความซ้ำซากจำเจ: . ลองเลือกจุดควบคุมหนึ่งจุดในแต่ละจุดแล้วค้นหาเครื่องหมายของอนุพันธ์ ณ จุดนี้
มีอยู่บนเส้นจำนวนทั้งหมดด้วย ดังนั้นในกรณีนี้ จุดวิกฤตจึงเป็นเพียงจุดที่สำคัญเท่านั้น เช่น จากที่ไหน และ . จุดวิกฤติและแบ่งโดเมนทั้งหมดของคำจำกัดความของฟังก์ชันออกเป็นสามช่วงของความซ้ำซากจำเจ: . ลองเลือกจุดควบคุมหนึ่งจุดในแต่ละจุดแล้วค้นหาเครื่องหมายของอนุพันธ์ ณ จุดนี้
สำหรับช่วงเวลานั้น จุดควบคุมสามารถเป็น: ค้นหา เมื่อหาจุดในช่วงเวลา เราก็ได้ และเมื่อถึงจุดในช่วงเวลา เราก็ได้ ดังนั้น ในช่วงเวลา และ และ ในช่วงเวลา ตามเกณฑ์แรกเพียงพอสำหรับค่าสุดขีด ไม่มีค่าสุดขีดที่จุด (เนื่องจากอนุพันธ์ยังคงมีเครื่องหมายอยู่ในช่วง) และ ณ จุดที่ฟังก์ชันมีค่าต่ำสุด (เนื่องจากอนุพันธ์เปลี่ยนเครื่องหมายจากลบเป็นบวกเมื่อส่งผ่าน ผ่านจุดนี้) มาหาค่าที่สอดคล้องกันของฟังก์ชันกัน: , a . ในช่วงเวลา ฟังก์ชันจะลดลง เนื่องจากในช่วงเวลานี้ และในช่วงเวลานั้นจะเพิ่มขึ้น เนื่องจากในช่วงเวลานี้
เพื่อชี้แจงโครงสร้างของกราฟ เราจะหาจุดตัดของมันด้วยแกนพิกัด เมื่อเราได้รับสมการที่มีรากเป็น และ คือพบสองจุด (0; 0) และ (4; 0) ของกราฟของฟังก์ชัน เราสร้างกราฟโดยใช้ข้อมูลทั้งหมดที่ได้รับ (ดูตอนต้นของตัวอย่าง)
คุณสามารถใช้การตรวจสอบตนเองระหว่างการคำนวณได้ เครื่องคิดเลขอนุพันธ์ออนไลน์ .

ตัวอย่างที่ 4หาจุดสุดขีดของฟังก์ชันแล้วสร้างกราฟของมัน
โดเมนของคำจำกัดความของฟังก์ชันคือเส้นจำนวนทั้งหมด ยกเว้นจุด นั่นคือ .
เพื่อให้การศึกษาสั้นลง คุณสามารถใช้ข้อเท็จจริงที่ว่าฟังก์ชันนี้เป็นเลขคู่ เนื่องจาก  . ดังนั้นกราฟของมันจึงสมมาตรรอบแกน เฮ้ยและการศึกษาสามารถทำได้เฉพาะช่วงเวลาเท่านั้น
. ดังนั้นกราฟของมันจึงสมมาตรรอบแกน เฮ้ยและการศึกษาสามารถทำได้เฉพาะช่วงเวลาเท่านั้น
การหาอนุพันธ์ ![]() และจุดวิกฤตของฟังก์ชัน:
และจุดวิกฤตของฟังก์ชัน:
1)  ;
;
2) ![]() ,
,
แต่ฟังก์ชันประสบปัญหาความไม่ต่อเนื่อง ณ จุดนี้ ดังนั้นจึงไม่สามารถเป็นจุดสุดขั้วได้
ดังนั้น ฟังก์ชันที่กำหนดจึงมีจุดวิกฤตสองจุด: และ เมื่อคำนึงถึงความเท่าเทียมกันของฟังก์ชัน เราจะตรวจสอบเฉพาะจุดโดยใช้เกณฑ์ที่สองที่เพียงพอสำหรับจุดสุดโต่ง เมื่อต้องการทำเช่นนี้ เราจะหาอนุพันธ์อันดับสอง ![]() และกำหนดสัญญาณได้ที่: เราได้รับ . เนื่องจาก และ มันคือจุดต่ำสุดของฟังก์ชัน และ
และกำหนดสัญญาณได้ที่: เราได้รับ . เนื่องจาก และ มันคือจุดต่ำสุดของฟังก์ชัน และ ![]() .
.
เพื่อให้เห็นภาพกราฟของฟังก์ชันที่สมบูรณ์ยิ่งขึ้น เรามาดูพฤติกรรมของมันที่ขอบเขตของโดเมนคำจำกัดความกันดีกว่า:

(ในที่นี้สัญลักษณ์แสดงถึงความปรารถนา xเป็นศูนย์จากทางขวา และ xยังคงเป็นบวก ในทำนองเดียวกันหมายถึงความทะเยอทะยาน xให้เป็นศูนย์จากทางซ้าย และ xยังคงเป็นลบ) ดังนั้น ถ้า แล้ว . ต่อไปเราจะพบ
 ,
,
เหล่านั้น. ถ้าอย่างนั้น
กราฟของฟังก์ชันไม่มีจุดตัดกับแกน รูปภาพอยู่ที่จุดเริ่มต้นของตัวอย่าง
คุณสามารถใช้การตรวจสอบตนเองระหว่างการคำนวณได้ เครื่องคิดเลขอนุพันธ์ออนไลน์ .
เรายังคงค้นหา extrema ของฟังก์ชันร่วมกันต่อไป
ตัวอย่างที่ 8ค้นหาจุดสุดขีดของฟังก์ชัน

สารละลาย. ลองหาโดเมนของนิยามของฟังก์ชันกัน เนื่องจากความไม่เท่าเทียมกันจะต้องได้รับการตอบสนอง เราจึงได้มาจาก
ลองหาอนุพันธ์อันดับหนึ่งของฟังก์ชันกัน
พิจารณากราฟของฟังก์ชันต่อเนื่อง y=ฉ(x)แสดงในรูป
ค่าฟังก์ชัน ณ จุดหนึ่ง x 1 จะมากกว่าค่าฟังก์ชันที่จุดใกล้เคียงทั้งหมดทั้งด้านซ้ายและด้านขวาของ x 1. ในกรณีนี้เราบอกว่าฟังก์ชันมีตรงประเด็น xสูงสุด 1 ตรงจุด xเห็นได้ชัดว่าฟังก์ชั่น 3 มีจำนวนสูงสุดเช่นกัน ถ้าเราพิจารณาประเด็นแล้ว x 2 ดังนั้นค่าฟังก์ชันในนั้นจะน้อยกว่าค่าใกล้เคียงทั้งหมด ในกรณีนี้เราบอกว่าฟังก์ชันมีตรงประเด็น xขั้นต่ำ 2 ในทำนองเดียวกันสำหรับประเด็น x 4 .
การทำงาน y=ฉ(x)ตรงจุด x 0 มี ขีดสุดหากค่าของฟังก์ชัน ณ จุดนี้มากกว่าค่าของฟังก์ชัน ณ จุดทั้งหมดที่มีจุดนั้นอยู่ x 0 เช่น หากมีบริเวณใกล้จุดดังกล่าว x 0 ซึ่งเหมาะสำหรับทุกคน x≠x 0 , ที่อยู่ในละแวกนี้ก็มีความไม่เท่าเทียมกัน ฉ(x)<ฉ(x 0 ) .
การทำงาน y=ฉ(x)มันมี ขั้นต่ำตรงจุด x 0 , หากมีบริเวณใกล้จุดดังกล่าว x 0 , นั่นสำหรับทุกคน x≠x 0 อยู่ในละแวกนี้ ความไม่เท่าเทียมกันยังคงอยู่ ฉ(x)>ฉ(x 0.
จุดที่ฟังก์ชันถึงค่าสูงสุดและต่ำสุดเรียกว่าจุดสุดขีดและค่าของฟังก์ชันที่จุดเหล่านี้เรียกว่าจุดสุดขีดของฟังก์ชัน
ให้เราใส่ใจกับความจริงที่ว่าฟังก์ชันที่กำหนดไว้ในเซ็กเมนต์สามารถเข้าถึงสูงสุดและต่ำสุดได้เฉพาะจุดที่อยู่ในเซ็กเมนต์ที่อยู่ระหว่างการพิจารณาเท่านั้น
โปรดทราบว่าหากฟังก์ชันมีค่าสูงสุดที่จุดหนึ่ง ไม่ได้หมายความว่า ณ จุดนั้นฟังก์ชันจะมีค่ามากที่สุดในขอบเขตคำจำกัดความทั้งหมด จากรูปที่กล่าวข้างต้น ฟังก์ชัน ณ จุดนั้น x 1 มีค่าสูงสุดแม้ว่าจะมีจุดที่ค่าฟังก์ชันมากกว่าจุดนั้นก็ตาม x 1 . โดยเฉพาะอย่างยิ่ง, ฉ(x 1) < ฉ(x 4) เช่น ค่าต่ำสุดของฟังก์ชันมากกว่าค่าสูงสุด จากคำจำกัดความของค่าสูงสุด จะตามมาเพียงว่านี่เป็นค่าที่ใหญ่ที่สุดของฟังก์ชันที่จุดที่ใกล้กับจุดสูงสุดเพียงพอ
ทฤษฎีบท 1 (เงื่อนไขที่จำเป็นสำหรับการมีอยู่ของสุดขั้ว)ถ้าฟังก์ชันหาอนุพันธ์ได้ y=ฉ(x)มีตรงจุด x= x 0 สุดขั้ว แล้วอนุพันธ์ของมัน ณ จุดนี้จะกลายเป็นศูนย์
การพิสูจน์. ให้ตรงจุดอย่างแน่นอน xฟังก์ชัน 0 มีจำนวนสูงสุด จากนั้นสำหรับการเพิ่มทีละน้อยเพียงพอ Δ xเรามี ฉ(x 0 + Δ เอ็กซ์)
ผ่านความไม่เท่าเทียมกันเหล่านี้ไปจนถึงขีดจำกัดที่ Δ x→ 0 และคำนึงถึงอนุพันธ์ด้วย ฉ "(x 0) มีอยู่ ดังนั้นขีดจำกัดทางด้านซ้ายจึงไม่ขึ้นอยู่กับว่า Δ เป็นอย่างไร x→ 0 เราได้: ที่ Δ x → 0 – 0 ฉ"(x 0) ≥ 0 a ที่Δ x → 0 + 0 ฉ"(x 0) ≤ 0 เนื่องจาก ฉ"(x 0) กำหนดตัวเลข ดังนั้นอสมการทั้งสองนี้จะเข้ากันได้ก็ต่อเมื่อ ฉ"(x 0) = 0.
ทฤษฎีบทที่ได้รับการพิสูจน์แล้วระบุว่าคะแนนสูงสุดและต่ำสุดสามารถอยู่ในค่าของการโต้แย้งที่อนุพันธ์กลายเป็นศูนย์เท่านั้น
เราพิจารณากรณีที่ฟังก์ชันมีอนุพันธ์ที่ทุกจุดของเซกเมนต์หนึ่งๆ กรณีที่ไม่มีอนุพันธ์จะเป็นอย่างไร? ลองดูตัวอย่าง
ตัวอย่าง.
- ย=|x|.
ฟังก์ชันไม่มีอนุพันธ์ ณ จุดนั้น x=0 ( ณ จุดนี้ กราฟของฟังก์ชันไม่มีค่าแทนเจนต์ที่กำหนดไว้) แต่ ณ จุดนี้ ฟังก์ชันมีค่าต่ำสุด เนื่องจาก ย(0)=0 และสำหรับทั้งหมด x≠ 0ย > 0.
- อนุญาต x< x
0 . แล้ว ค< x
0 และ ฉ "(ค)> 0.
นั่นเป็นเหตุผล ฉ "(ค)(x- x 0)<
0 และดังนั้น
ฉ(x) - ฉ(x 0 )< 0 เช่น ฉ(x)< f(x 0 ).
- อนุญาต x > x 0 . แล้ว ค>x 0 และ ฉ "(ค)< 0. วิธี ฉ "(ค)(x- x 0)< 0. นั่นเป็นเหตุผล ฉ(x) - ฉ(x 0 ) <0,т.е.ฉ(x)< ฉ(x 0 ) .
- ค้นหาโดเมนของฟังก์ชัน ฉ(x)
- ค้นหาอนุพันธ์อันดับหนึ่งของฟังก์ชัน ฉ "(x).
- กำหนดจุดวิกฤติสำหรับสิ่งนี้:
- ค้นหารากที่แท้จริงของสมการ ฉ "(x)=0;
- ค้นหาค่าทั้งหมด xซึ่งอนุพันธ์นั้น ฉ "(x)ไม่ได้อยู่.
- กำหนดเครื่องหมายของอนุพันธ์ทางซ้ายและขวาของจุดวิกฤต เนื่องจากเครื่องหมายของอนุพันธ์ยังคงที่ระหว่างจุดวิกฤตสองจุด จึงเพียงพอที่จะระบุเครื่องหมายของอนุพันธ์ที่จุดหนึ่งทางซ้ายและอีกจุดทางด้านขวาของจุดวิกฤติ
- คำนวณค่าของฟังก์ชันที่จุดปลายสุด
- ค้นหาจุดวิกฤตทั้งหมดของฟังก์ชันในช่วงเวลา ( ก, ข) และคำนวณค่าของฟังก์ชันที่จุดเหล่านี้
- คำนวณค่าของฟังก์ชันที่ส่วนท้ายของเซ็กเมนต์เมื่อใด x = ก, x = ข.
- จากค่าที่ได้รับทั้งหมด ให้เลือกค่าที่ใหญ่ที่สุดและเล็กที่สุด
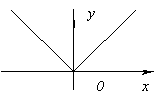
ฟังก์ชันไม่มีอนุพันธ์ที่ x=0 เนื่องจากมันจะไปถึงอนันต์ที่ x=0. แต่ ณ จุดนี้ฟังก์ชันจะมีค่าสูงสุด
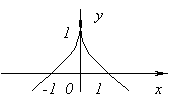
ฟังก์ชันไม่มีอนุพันธ์ที่ x=0 เนื่องจาก ![]() ที่ x→0. ณ จุดนี้ฟังก์ชันไม่มีค่าสูงสุดหรือค่าต่ำสุด จริงหรือ, ฉ(x)=0 และที่ x<0ฉ(x)<0, а при x>0ฉ(x)>0.
ที่ x→0. ณ จุดนี้ฟังก์ชันไม่มีค่าสูงสุดหรือค่าต่ำสุด จริงหรือ, ฉ(x)=0 และที่ x<0ฉ(x)<0, а при x>0ฉ(x)>0.

ดังนั้น จากตัวอย่างที่ให้ไว้และทฤษฎีบทที่ถูกกำหนดไว้ เห็นได้ชัดว่าฟังก์ชันสามารถมีจุดสุดขั้วได้เพียงสองกรณีเท่านั้น: 1) ณ จุดที่มีอนุพันธ์อยู่และเท่ากับศูนย์; 2) ณ จุดที่ไม่มีอนุพันธ์อยู่
อย่างไรก็ตามหากถึงจุดใดจุดหนึ่ง x 0 เรารู้สิ่งนั้น ฉ "(x 0 ) =0 จึงไม่สามารถสรุปได้ว่า ณ จุดนั้น x 0 ฟังก์ชันมีปลายสุด
ตัวอย่างเช่น. ![]() .
.

แต่ช่วง x=0 ไม่ใช่จุดสุดขั้ว เนื่องจากทางด้านซ้ายของจุดนี้ ค่าฟังก์ชันจะอยู่ใต้แกน วัวและทางด้านขวาด้านบน
ค่าของอาร์กิวเมนต์จากโดเมนของฟังก์ชันที่อนุพันธ์ของฟังก์ชันหายไปหรือไม่มีอยู่เรียกว่า จุดวิกฤติ.
จากที่กล่าวมาทั้งหมด จุดปลายสุดของฟังก์ชันจะอยู่ในหมู่จุดวิกฤต อย่างไรก็ตาม ไม่ใช่ทุกจุดวิกฤติที่จะเป็นจุดปลายสุด ดังนั้น ในการค้นหาจุดปลายสุดของฟังก์ชัน คุณจะต้องค้นหาจุดวิกฤตทั้งหมดของฟังก์ชัน จากนั้นจึงตรวจสอบแต่ละจุดแยกกันเพื่อหาค่าสูงสุดและค่าต่ำสุด ทฤษฎีบทต่อไปนี้มีจุดประสงค์นี้
ทฤษฎีบท 2 (เงื่อนไขที่เพียงพอสำหรับการดำรงอยู่ของสุดขั้ว)ปล่อยให้ฟังก์ชันต่อเนื่องในช่วงเวลาหนึ่งที่มีจุดวิกฤติ x 0 และสามารถหาอนุพันธ์ได้ในทุกจุดของช่วงเวลานี้ (ยกเว้น บางทีอาจจะเป็นจุดนั้นเอง) x 0) เมื่อย้ายจากซ้ายไปขวาผ่านจุดนี้ ถ้าอนุพันธ์เปลี่ยนเครื่องหมายจากบวกเป็นลบ แล้วถึงจุดนั้น x = xฟังก์ชัน 0 มีจำนวนสูงสุด หากเมื่อผ่าน. x 0 จากซ้ายไปขวา อนุพันธ์เปลี่ยนเครื่องหมายจากลบเป็นบวก แล้วฟังก์ชันจะมีค่าต่ำสุด ณ จุดนี้
ดังนั้นหาก
การพิสูจน์. ให้เราสันนิษฐานไว้ก่อนว่าเมื่อผ่านไปแล้ว x 0 อนุพันธ์เปลี่ยนเครื่องหมายจากบวกเป็นลบ เช่น ต่อหน้าทุกคน x,ใกล้จุด x 0 ฉ "(x)> 0 สำหรับ x< x 0 , ฉ "(x)< 0 สำหรับ x> x 0 . ลองใช้ทฤษฎีบทของลากรองจ์กับความแตกต่างกัน ฉ(x) - ฉ(x 0 ) = ฉ "(ค)(x- x 0) ที่ไหน คอยู่ระหว่าง xและ x 0 .
ดังนั้นสำหรับทุกค่า xใกล้พอที่จะ x 0 ฉ(x)< ฉ(x 0 ) . และนี่หมายความว่า ณ จุดนั้น xฟังก์ชัน 0 มีจำนวนสูงสุด
ส่วนที่สองของทฤษฎีบทขั้นต่ำก็พิสูจน์ในลักษณะเดียวกัน
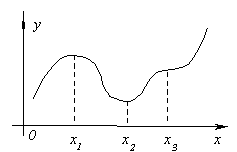
ให้เราอธิบายความหมายของทฤษฎีบทนี้ในรูป อนุญาต ฉ "(x 1 ) =0 และสำหรับใดๆ เอ็กซ์,ใกล้พอที่จะ x 1 ความไม่เท่าเทียมกันมีความพึงพอใจ
ฉ "(x)< 0 ณ x< x 1 , ฉ "(x)> 0 ณ x> x 1 .
จากนั้นไปทางซ้ายของจุด x 1 ฟังก์ชั่นจะเพิ่มขึ้นและลดลงทางด้านขวา ดังนั้นเมื่อใด x = x 1 ฟังก์ชันเปลี่ยนจากเพิ่มขึ้นไปสู่ลดลง นั่นคือมีค่าสูงสุด
ในทำนองเดียวกัน เราสามารถพิจารณาประเด็นต่างๆ ได้ x 2 และ x 3 .

ทั้งหมดข้างต้นสามารถแสดงเป็นแผนผังในภาพ:
กฎสำหรับการศึกษาฟังก์ชัน y=f(x) สำหรับส่วนปลายสุด
ตัวอย่าง. สำรวจฟังก์ชันสำหรับค่าต่ำสุดและสูงสุด
ค่าสูงสุดและค่าน้อยที่สุดของฟังก์ชันบนเซ็กเมนต์
ที่ใหญ่ที่สุดค่าของฟังก์ชันในช่วงเวลาหนึ่งจะใหญ่ที่สุดจากค่าทั้งหมดในช่วงเวลานี้และ ที่เล็กที่สุด– ค่าที่น้อยที่สุดในบรรดาค่าทั้งหมด
พิจารณาฟังก์ชัน y=ฉ(x)ต่อเนื่องในส่วน [ ก, ข] ดังที่ทราบ ฟังก์ชันดังกล่าวถึงค่าสูงสุดและต่ำสุด ไม่ว่าจะอยู่ที่ขอบเขตของเซ็กเมนต์หรือภายในนั้น หากค่าสูงสุดหรือต่ำสุดของฟังก์ชันบรรลุถึงจุดภายในของเซ็กเมนต์ ค่านี้จะเป็นค่าสูงสุดหรือต่ำสุดของฟังก์ชัน กล่าวคือ ค่าดังกล่าวบรรลุที่จุดวิกฤต
ดังนั้นเราจึงได้สิ่งต่อไปนี้ กฎสำหรับการค้นหาค่าที่ใหญ่ที่สุดและน้อยที่สุดของฟังก์ชันในส่วน [ ก, ข] :