Crescente, decrescente e extremos de uma função

Encontrar os intervalos de aumento, diminuição e extremos de uma função é uma tarefa independente e uma parte essencial de outras tarefas, em particular, estudo de função completa. As informações iniciais sobre o aumento, diminuição e extremos da função são fornecidas em capítulo teórico sobre derivada, que eu recomendo fortemente para estudo preliminar (ou repetição)– também pela razão de que o seguinte material é baseado no próprio essencialmente derivado, sendo uma continuação harmoniosa deste artigo. Embora, se o tempo for curto, também será possível uma prática puramente formal dos exemplos da lição de hoje.

E hoje há um espírito de rara unanimidade no ar, e posso sentir diretamente que todos os presentes estão ardendo de desejo aprenda a explorar uma função usando sua derivada. Portanto, uma terminologia razoável, boa e eterna aparece imediatamente nas telas do seu monitor.

Para que? Um dos motivos é o mais prático: para que fique claro o que geralmente é exigido de você em uma tarefa específica!

Monotonicidade da função. Pontos extremos e extremos de uma função

Vamos considerar alguma função. Simplificando, assumimos que ela contínuo em toda a reta numérica:

Por precaução, vamos nos livrar imediatamente de possíveis ilusões, principalmente para os leitores que recentemente conheceram intervalos de sinal constante da função. Agora nós NÃO INTERESSADO, como o gráfico da função está localizado em relação ao eixo (acima, abaixo, onde o eixo se cruza). Para ser convincente, apague mentalmente os eixos e deixe um gráfico. Porque é aí que reside o interesse.

Função aumenta em um intervalo se para quaisquer dois pontos deste intervalo conectados pela relação, a desigualdade é verdadeira. Ou seja, um valor maior do argumento corresponde a um valor maior da função, e seu gráfico vai “de baixo para cima”. A função de demonstração cresce ao longo do intervalo.

Da mesma forma, a função diminui em um intervalo se para quaisquer dois pontos de um determinado intervalo tal que, a desigualdade é verdadeira. Ou seja, um valor maior do argumento corresponde a um valor menor da função, e seu gráfico vai “de cima para baixo”. Nossa função diminui em intervalos .

Se uma função aumenta ou diminui em um intervalo, ela é chamada estritamente monótono neste intervalo. O que é monotonia? Leve literalmente – monotonia.

Você também pode definir não decrescente função (condição relaxada na primeira definição) e não crescente função (condição suavizada na 2ª definição). Uma função não decrescente ou não crescente em um intervalo é chamada de função monotônica em um determinado intervalo (monotonicidade estrita é um caso especial de monotonicidade “simplesmente”).

A teoria também considera outras abordagens para determinar o aumento/diminuição de uma função, inclusive em meios intervalos, segmentos, mas para não derramar óleo-óleo-óleo na sua cabeça, concordaremos em operar com intervalos abertos com definições categóricas - isso é mais claro e é suficiente para resolver muitos problemas práticos.

Por isso, em meus artigos a expressão “monotonicidade de uma função” quase sempre estará oculta intervalos monotonia estrita(função estritamente crescente ou estritamente decrescente).

Vizinhança de um ponto. Palavras após as quais os alunos fogem para onde podem e se escondem horrorizados nos cantos. ...Embora depois da postagem Limites de Cauchy Eles provavelmente não estão mais se escondendo, apenas estremecendo levemente =) Não se preocupe, agora não haverá provas dos teoremas da análise matemática - eu precisava do ambiente para formular as definições de forma mais estrita pontos extremos. Vamos lembrar:

Bairro de um ponto um intervalo que contém um determinado ponto é chamado e, por conveniência, o intervalo é frequentemente considerado simétrico. Por exemplo, um ponto e sua vizinhança padrão:

Na verdade, as definições:

O ponto é chamado ponto máximo estrito, Se existe seu bairro, para todos valores dos quais, exceto o próprio ponto, a desigualdade . Em nosso exemplo específico, isso é um ponto.

O ponto é chamado ponto mínimo estrito, Se existe seu bairro, para todos valores dos quais, exceto o próprio ponto, a desigualdade . No desenho há o ponto “a”.

Observação : o requisito de simetria de vizinhança não é de todo necessário. Além disso, é importante o próprio fato da existência vizinhança (seja minúscula ou microscópica) que satisfaça as condições especificadas

Os pontos são chamados pontos estritamente extremos ou simplesmente pontos extremos funções. Ou seja, é um termo generalizado para pontos máximos e pontos mínimos.

Como entendemos a palavra “extremo”? Sim, tão diretamente quanto a monotonia. Pontos extremos de montanhas-russas.

Como no caso da monotonicidade, existem postulados vagos e são ainda mais comuns na teoria (que, é claro, se enquadram nos casos estritos considerados!):

O ponto é chamado ponto máximo, Se existe seu entorno é tal que para todos
O ponto é chamado ponto mínimo, Se existe seu entorno é tal que para todos valores desta vizinhança, a desigualdade se mantém.

Observe que de acordo com as duas últimas definições, qualquer ponto de uma função constante (ou uma “seção plana” de uma função) é considerado um ponto máximo e um ponto mínimo! A função, aliás, é não crescente e não decrescente, ou seja, monotônica. Contudo, deixaremos estas considerações para os teóricos, pois na prática quase sempre contemplamos os tradicionais “morros” e “depressões” (ver desenho) com um único “rei do morro” ou “princesa do pântano”. Como variedade, ocorre dica, direcionado para cima ou para baixo, por exemplo, o mínimo da função no ponto.

Ah, e falando em realeza:
– o significado é chamado máximo funções;
– o significado é chamado mínimo funções.

Nome comum - extremos funções.

Por favor, tenha cuidado com suas palavras!

Pontos extremos– estes são valores “X”.
Extremos– significados de “jogo”.

! Observação : às vezes, os termos listados referem-se aos pontos “XY” que estão diretamente no GRÁFICO DA PRÓPRIA função.

Quantos extremos uma função pode ter?

Nenhum, 1, 2, 3, ... etc. ao infinito. Por exemplo, o seno tem infinitos mínimos e máximos.

IMPORTANTE! O termo "máximo de função" não idênticos o termo “valor máximo de uma função”. É fácil perceber que o valor é máximo apenas em um bairro local, e no canto superior esquerdo estão “camaradas mais legais”. Da mesma forma, “mínimo de uma função” não é o mesmo que “valor mínimo de uma função”, e no desenho vemos que o valor é mínimo apenas em uma determinada área. A este respeito, os pontos extremos também são chamados pontos extremos locais, e os extremos - extremos locais. Eles andam e vagam por perto e global irmãos. Então, qualquer parábola tem no seu vértice mínimo global ou máximo global. Além disso, não farei distinção entre tipos de extremos, e a explicação é expressa mais para fins educacionais gerais - os adjetivos adicionais “local”/“global” não devem pegá-lo de surpresa.

Vamos resumir nossa breve excursão pela teoria com um teste: o que significa a tarefa “encontrar os intervalos de monotonicidade e os pontos extremos da função”?

O texto incentiva você a encontrar:

– intervalos de função crescente/decrescente (não decrescente, não crescente aparece com muito menos frequência);

– pontos máximos e/ou mínimos (se existirem). Bem, para evitar falhas, é melhor encontrar os próprios mínimos/máximos ;-)

Como determinar tudo isso? Usando a função derivada!

Como encontrar intervalos de aumento, diminuição,
pontos extremos e extremos da função?

Muitas regras, na verdade, já são conhecidas e compreendidas desde lição sobre o significado de uma derivada.

Derivada tangente traz a boa notícia de que a função está aumentando em todo domínio de definição.

Com cotangente e sua derivada a situação é exatamente oposta.

O arco seno aumenta ao longo do intervalo - a derivada aqui é positiva: .
Quando a função é definida, mas não diferenciável. No entanto, no ponto crítico há uma derivada destra e uma tangente destra, e na outra aresta estão suas contrapartes canhotas.

Penso que não será muito difícil para si realizar um raciocínio semelhante para o arco cosseno e a sua derivada.

Todos os casos acima, muitos dos quais são derivadas tabulares, lembro a você, siga diretamente de definições derivadas.

Por que explorar uma função usando sua derivada?

Para entender melhor como é o gráfico desta função: onde vai “de baixo para cima”, onde “de cima para baixo”, onde atinge mínimos e máximos (se é que atinge). Nem todas as funções são tão simples - na maioria dos casos não temos ideia alguma sobre o gráfico de uma função específica.

É hora de passar para exemplos mais significativos e considerar algoritmo para encontrar intervalos de monotonicidade e extremos de uma função:

Exemplo 1

Encontre intervalos de aumento/diminuição e extremos da função

Solução:

1) O primeiro passo é encontrar domínio de uma função e também anote os pontos de interrupção (se existirem). Neste caso, a função é contínua em toda a reta numérica e esta ação é até certo ponto formal. Mas em vários casos, paixões sérias surgem aqui, então vamos tratar o parágrafo sem desdém.

2) O segundo ponto do algoritmo se deve a

uma condição necessária para um extremo:

Se houver um extremo em um ponto, então o valor não existe.

Ficou confuso com o final? Extremo da função “módulo x” .

A condição é necessária, mas insuficiente, e o inverso nem sempre é verdadeiro. Portanto, ainda não decorre da igualdade que a função atinja um máximo ou um mínimo no ponto . Um exemplo clássico já foi destacado acima - esta é uma parábola cúbica e seu ponto crítico.

Mas seja como for, a condição necessária para um extremo dita a necessidade de encontrar pontos suspeitos. Para fazer isso, encontre a derivada e resolva a equação:

No início do primeiro artigo sobre gráficos de funções Eu lhe disse como construir rapidamente uma parábola usando um exemplo : “...pegamos a primeira derivada e igualamos a zero: ...Então, a solução da nossa equação: - é neste ponto que se localiza o vértice da parábola...”. Agora, acho que todos entendem porque o vértice da parábola está localizado exatamente neste ponto =) Em geral, deveríamos começar com um exemplo semelhante aqui, mas é muito simples (mesmo para um bule de chá). Além disso, há um análogo no final da lição sobre derivada de uma função. Portanto, vamos aumentar o grau:

Exemplo 2

Encontre intervalos de monotonicidade e extremos da função

Este é um exemplo para você resolver sozinho. Uma solução completa e uma amostra final aproximada do problema no final da lição.

Chegou o tão esperado momento de encontro com funções racionais fracionárias:

Exemplo 3

Explore uma função usando a primeira derivada

Preste atenção em como uma mesma tarefa pode ser reformulada de forma variável.

Solução:

1) A função sofre infinitas descontinuidades em pontos.

2) Detectamos pontos críticos. Vamos encontrar a primeira derivada e igualá-la a zero:

Vamos resolver a equação. Uma fração é zero quando seu numerador é zero:

Assim, obtemos três pontos críticos:

3) Plotamos TODOS os pontos detectados na reta numérica e método de intervalo definimos os sinais da DERIVATIVA:

Deixe-me lembrá-lo de que você precisa pegar algum ponto do intervalo e calcular o valor da derivada nele e determine seu sinal. É mais lucrativo nem contar, mas “estimar” verbalmente. Vamos pegar, por exemplo, um ponto pertencente ao intervalo e realizar a substituição: .

Dois “mais” e um “menos” dão um “menos”, portanto, o que significa que a derivada é negativa em todo o intervalo.

A ação, como você entende, precisa ser realizada em cada um dos seis intervalos. A propósito, observe que o fator numerador e o denominador são estritamente positivos para qualquer ponto em qualquer intervalo, o que simplifica bastante a tarefa.

Então, a derivada nos disse que a PRÓPRIA FUNÇÃO aumenta em e diminui em . É conveniente conectar intervalos do mesmo tipo com o ícone de junção.

No ponto em que a função atinge seu máximo:
No ponto em que a função atinge o mínimo:

Pense por que você não precisa recalcular o segundo valor ;-)

Ao passar por um ponto, a derivada não muda de sinal, então a função NÃO TEM EXTREMO ali - ela diminuiu e permaneceu decrescente.

! Vamos repetir um ponto importante: os pontos não são considerados críticos - eles contêm uma função não determinado. Assim, aqui Em princípio não pode haver extremos(mesmo que a derivada mude de sinal).

Responder: a função aumenta em e diminui em No ponto em que o máximo da função é atingido: , e no ponto – o mínimo: .

Conhecimento de intervalos e extremos de monotonicidade, juntamente com assíntotas já dá uma ideia muito boa da aparência do gráfico da função. Uma pessoa com treinamento médio é capaz de determinar verbalmente que o gráfico de uma função tem duas assíntotas verticais e uma assíntota oblíqua. Aqui está nosso herói:

Tente mais uma vez correlacionar os resultados do estudo com o gráfico desta função.
Não há extremo no ponto crítico, mas há inflexão do gráfico(o que, via de regra, acontece em casos semelhantes).

Exemplo 4

Encontre os extremos da função

Exemplo 5

Encontre intervalos de monotonicidade, máximos e mínimos da função

…é quase como uma espécie de feriado “X em um cubo” hoje....
Entããão, quem na galeria se ofereceu para beber por isso? =)

Cada tarefa tem suas próprias nuances substantivas e sutilezas técnicas, que são comentadas no final da lição.

Monótono

Uma propriedade muito importante de uma função é a sua monotonicidade. Conhecendo esta propriedade de diversas funções especiais, é possível determinar o comportamento de diversos processos físicos, econômicos, sociais e muitos outros.

Os seguintes tipos de monotonia de funções são diferenciados:

1) função aumenta, se em um determinado intervalo, se para quaisquer dois pontos e esse intervalo for tal que. Aqueles. um valor de argumento maior corresponde a um valor de função maior;

2) função diminui, se em um determinado intervalo, se para quaisquer dois pontos e esse intervalo for tal que. Aqueles. um valor de argumento maior corresponde a um valor de função menor;

3) função não decrescente, se em um determinado intervalo, se para quaisquer dois pontos e este intervalo for tal que ;

4) função não aumenta, se em um determinado intervalo, se para quaisquer dois pontos e esse intervalo for tal que.

2. Para os dois primeiros casos, também é utilizado o termo “monotonicidade estrita”.

3. Os dois últimos casos são específicos e normalmente especificados como uma composição de diversas funções.

4. Separadamente, notamos que o aumento e a diminuição do gráfico de uma função devem ser considerados da esquerda para a direita e nada mais.

2. Par ou ímpar.

A função é chamada ímpar, se quando o sinal do argumento muda, ele muda seu valor para o oposto. A fórmula para isso é semelhante a esta . Isso significa que depois de substituir os valores “menos x” na função no lugar de todos os x, a função mudará seu sinal. O gráfico de tal função é simétrico em relação à origem.

Exemplos de funções ímpares são etc.

Por exemplo, o gráfico na verdade tem simetria em relação à origem:

A função é chamada par, se quando o sinal do argumento muda, ele não altera seu valor. A fórmula para isso é semelhante a esta. Isso significa que depois de substituir os valores “menos x” na função no lugar de todos os x, a função não mudará como resultado. O gráfico de tal função é simétrico em relação ao eixo.

Exemplos de funções pares são etc.

Por exemplo, vamos mostrar a simetria do gráfico em relação ao eixo:

Se uma função não pertence a nenhum dos tipos especificados, então ela não é chamada de par, nem ímpar ou função geral. Tais funções não têm simetria.

Tal função, por exemplo, é a função linear que consideramos recentemente com um gráfico:

3. Uma propriedade especial das funções é periodicidade.

O fato é que as funções periódicas consideradas no currículo escolar padrão são apenas funções trigonométricas. Já falamos sobre eles em detalhes ao estudar o tema relevante.

Função periódicaé uma função que não altera seus valores quando um certo número constante diferente de zero é adicionado ao argumento.

Este número mínimo é chamado período da função e são designados pela letra .

A fórmula para isso é semelhante a esta: .

Vejamos esta propriedade usando o exemplo de um gráfico senoidal:

Lembremos que o período das funções e é , e o período e é .

Como já sabemos, funções trigonométricas com argumentos complexos podem ter um período não padronizado. Estamos falando de funções da forma:

O período deles é igual. E sobre as funções:

O período deles é igual.

Como você pode ver, para calcular um novo período, o período padrão é simplesmente dividido pelo fator do argumento. Não depende de outras modificações da função.

Limitação.

Função y=f(x) é chamado limitado por baixo no conjunto X⊂D(f) se existe um número a tal que para qualquer xϵX a desigualdade f(x) é válida< a.

Função y=f(x) é chamado limitado de cima no conjunto X⊂D(f) se existe um número a tal que para qualquer хϵХ a desigualdade f(x) é válida< a.

Se o intervalo X não for especificado, a função será considerada limitada em todo o domínio de definição. Uma função limitada acima e abaixo é chamada de limitada.

A limitação da função é fácil de ler no gráfico. Você pode desenhar alguma linha y=a, e se a função for superior a esta linha, ela será limitada por baixo.

Se abaixo, então acima. Abaixo está um gráfico de uma função limitada abaixo. Pessoal, tentem desenhar vocês mesmos um gráfico de uma função limitada.

Tópico: Propriedades das funções: intervalos crescentes e decrescentes; valores mais altos e mais baixos; pontos extremos (máximo e mínimo locais), convexidade da função.

Intervalos de aumento e diminuição.

Com base em condições suficientes (sinais) para o aumento e diminuição de uma função, são encontrados intervalos de aumento e diminuição da função.

Aqui estão as formulações dos sinais de funções crescentes e decrescentes em um intervalo:

· se a derivada da função y=f(x) positivo para qualquer um x do intervalo X, então a função aumenta em X;

· se a derivada da função y=f(x) negativo para qualquer um x do intervalo X, então a função diminui em X.

Assim, para determinar os intervalos de aumento e diminuição de uma função, é necessário:

· encontrar o domínio de definição da função;

· encontrar a derivada da função;

· resolver desigualdades no domínio da definição;

Extremos da função

Definição 2

Um ponto $x_0$ é chamado de ponto máximo de uma função $f(x)$ se existe uma vizinhança deste ponto tal que para todo $x$ nesta vizinhança a desigualdade $f(x)\le f(x_0) $ detém.

Definição 3

Um ponto $x_0$ é chamado de ponto máximo de uma função $f(x)$ se existe uma vizinhança deste ponto tal que para todo $x$ nesta vizinhança a desigualdade $f(x)\ge f(x_0) $ detém.

O conceito de extremo de uma função está intimamente relacionado ao conceito de ponto crítico de uma função. Vamos apresentar sua definição.

Definição 4

$x_0$ é chamado de ponto crítico da função $f(x)$ se:

1) $x_0$ – ponto interno do domínio de definição;

2) $f"\left(x_0\right)=0$ ou não existe.

Para o conceito de extremo, podemos formular teoremas sobre condições suficientes e necessárias para sua existência.

Teorema 2

Condição suficiente para um extremo

Seja o ponto $x_0$ crítico para a função $y=f(x)$ e esteja no intervalo $(a,b)$. Deixe em cada intervalo $\left(a,x_0\right)\ e\ (x_0,b)$ a derivada $f"(x)$ existe e mantém um sinal constante. Então:

1) Se no intervalo $(a,x_0)$ a derivada é $f"\left(x\right)>0$, e no intervalo $(x_0,b)$ a derivada é $f"\left( x\direita)

2) Se no intervalo $(a,x_0)$ a derivada $f"\left(x\right)0$, então o ponto $x_0$ é o ponto mínimo para esta função.

3) Se ambos no intervalo $(a,x_0)$ e no intervalo $(x_0,b)$ a derivada $f"\left(x\right) >0$ ou a derivada $f"\left(x \certo)

Este teorema é ilustrado na Figura 1.

Figura 1. Condição suficiente para existência de extremos

Exemplos de extremos (Fig. 2).

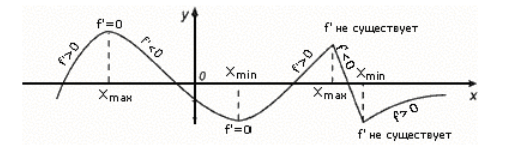
Figura 2. Exemplos de pontos extremos

Regra para estudar uma função para extremo

2) Encontre a derivada $f"(x)$;

7) Tire conclusões sobre a presença de máximos e mínimos em cada intervalo, utilizando o Teorema 2.

Função crescente e decrescente

Vamos primeiro apresentar as definições de funções crescentes e decrescentes.

Definição 5

Uma função $y=f(x)$ definida no intervalo $X$ é considerada crescente se para quaisquer pontos $x_1,x_2\in X$ em $x_1

Definição 6

Uma função $y=f(x)$ definida no intervalo $X$ é considerada decrescente se para quaisquer pontos $x_1,x_2\in X$ para $x_1f(x_2)$.

Estudando uma função para aumentar e diminuir

Você pode estudar funções crescentes e decrescentes usando a derivada.

Para examinar uma função para intervalos crescentes e decrescentes, você deve fazer o seguinte:

1) Encontre o domínio de definição da função $f(x)$;

2) Encontre a derivada $f"(x)$;

3) Encontre os pontos em que a igualdade $f"\left(x\right)=0$ é válida;

4) Encontre os pontos em que $f"(x)$ não existe;

5) Marcar na reta coordenada todos os pontos encontrados e o domínio de definição desta função;

6) Determine o sinal da derivada $f"(x)$ em cada intervalo resultante;

7) Tire uma conclusão: em intervalos onde $f"\left(x\right)0$ a função aumenta.

Exemplos de problemas para estudar funções crescentes, decrescentes e presença de pontos extremos

Exemplo 1

Examine a função de aumento e diminuição e a presença de pontos de máximo e mínimo: $f(x)=(2x)^3-15x^2+36x+1$

Como os primeiros 6 pontos são iguais, vamos realizá-los primeiro.

1) Domínio de definição – todos os números reais;

2) $f"\esquerda(x\direita)=6x^2-30x+36$;

3) $f"\esquerda(x\direita)=0$;

\ \ \

4) $f"(x)$ existe em todos os pontos do domínio de definição;

5) Linha de coordenadas:

Figura 3.

6) Determine o sinal da derivada $f"(x)$ em cada intervalo:

\ \ .

Condições suficientes para o extremo de uma função.

Para encontrar os máximos e mínimos de uma função, você pode usar qualquer um dos três sinais de extremo, é claro, se a função satisfizer suas condições. O mais comum e conveniente é o primeiro deles.

A primeira condição suficiente para um extremo.

Seja a função y=f(x) diferenciável na vizinhança do ponto e contínua no próprio ponto.

Em outras palavras:

Algoritmo para encontrar pontos extremos baseado no primeiro sinal de extremo de uma função.

• Encontramos o domínio de definição da função.
• Encontramos a derivada da função no domínio de definição.
• Determinamos os zeros do numerador, os zeros do denominador da derivada e os pontos do domínio de definição em que a derivada não existe (todos os pontos listados são chamados pontos de possível extremo, passando por esses pontos, a derivada pode simplesmente mudar de sinal).
• Esses pontos dividem o domínio de definição da função em intervalos nos quais a derivada mantém seu sinal. Determinamos os sinais da derivada em cada um dos intervalos (por exemplo, calculando o valor da derivada de uma função em qualquer ponto de um intervalo específico).
• Selecionamos pontos nos quais a função é contínua e, passando pelos quais, a derivada muda de sinal - esses são os pontos extremos.

Existem muitas palavras, vamos dar uma olhada em alguns exemplos de como encontrar pontos extremos e extremos de uma função usando a primeira condição suficiente para o extremo de uma função.

Exemplo.

Encontre os extremos da função.

Solução.

O domínio de uma função é todo o conjunto dos números reais, exceto x=2.

Encontrando a derivada:

Os zeros do numerador são os pontos x=-1 e x=5, o denominador vai para zero em x=2. Marque esses pontos no eixo numérico

Determinamos os sinais da derivada em cada intervalo; para isso calculamos o valor da derivada em qualquer um dos pontos de cada intervalo, por exemplo, nos pontos x=-2, x=0, x=3 e x=6.

Portanto, no intervalo a derivada é positiva (na figura colocamos um sinal de mais neste intervalo). Da mesma maneira

Portanto, colocamos menos acima do segundo intervalo, menos acima do terceiro e mais acima do quarto.

Resta selecionar os pontos nos quais a função é contínua e sua derivada muda de sinal. Esses são os pontos extremos.

No ponto x=-1 a função é contínua e a derivada muda de sinal de mais para menos, portanto, de acordo com o primeiro sinal do extremo, x=-1 é o ponto máximo, o máximo da função corresponde a ele .

No ponto x=5 a função é contínua e a derivada muda de sinal de menos para mais, portanto, x=-1 é o ponto mínimo, o mínimo da função corresponde a ele .

Ilustração gráfica.

Responder:

ATENÇÃO: o primeiro critério suficiente para um extremo não requer diferenciabilidade da função no próprio ponto.

Exemplo.

Encontre pontos extremos e extremos da função .

Solução.

O domínio de uma função é todo o conjunto dos números reais. A função em si pode ser escrita como:

Vamos encontrar a derivada da função:

No ponto x=0 a derivada não existe, pois os valores dos limites unilaterais não coincidem quando o argumento tende a zero:

Ao mesmo tempo, a função original é contínua no ponto x=0 (veja a seção sobre o estudo da função para continuidade):

Vamos encontrar o valor do argumento no qual a derivada vai para zero:

Vamos marcar todos os pontos obtidos na reta numérica e determinar o sinal da derivada em cada um dos intervalos. Para fazer isso, calculamos os valores da derivada em pontos arbitrários de cada intervalo, por exemplo, em x=-6, x=-4, x=-1, x=1, x=4, x=6.

Aquilo é,

Assim, de acordo com o primeiro sinal de um extremo, os pontos mínimos são , os pontos máximos são .

Calculamos os mínimos correspondentes da função

Calculamos os máximos correspondentes da função

Ilustração gráfica.

Responder:

.

O segundo sinal de um extremo de uma função.

Como você pode ver, este sinal de extremo de uma função requer a existência de uma derivada de pelo menos segunda ordem no ponto.

Função crescente e decrescente

função sim = f(x) é chamado de crescente no intervalo [ a, b], se para qualquer par de pontos X E X", a ≤ x a desigualdade é válida f(x) ≤ f (x"), e estritamente crescente - se a desigualdade f (x) f(x"). Funções decrescentes e estritamente decrescentes são definidas de forma semelhante. Por exemplo, a função no = X 2 (arroz. , a) aumenta estritamente no segmento , e

(arroz. , b) diminui estritamente neste segmento. Funções crescentes são designadas f (x) e diminuindo f (x)↓. Para que uma função diferenciável f (x) estava aumentando no segmento [ A, b], é necessário e suficiente que sua derivada f"(x) não foi negativo em [ A, b].

Juntamente com o aumento e a diminuição de uma função num segmento, consideramos o aumento e a diminuição de uma função num ponto. Função no = f (x) é chamado de crescente no ponto x 0 se houver um intervalo (α, β) contendo o ponto x 0, que para qualquer ponto X de (α, β), x> x 0 , a desigualdade é válida f (x 0) ≤ f (x), e para qualquer ponto X de (α, β), x 0 , a desigualdade é válida f (x) ≤f (x 0). O aumento estrito de uma função no ponto é definido de forma semelhante x 0. Se f"(x 0) > 0, então a função f(x) aumenta estritamente no ponto x 0. Se f (x) aumenta em cada ponto do intervalo ( a, b), então aumenta nesse intervalo.

SB Stechkin.

Grande Enciclopédia Soviética. - M.: Enciclopédia Soviética. 1969-1978 .

Veja o que são “Funções crescentes e decrescentes” em outros dicionários:

Conceitos de análise matemática. A função f(x) é chamada de razão entre o número de diferentes faixas etárias da população que aumenta no segmento ESTRUTURA ETÁRIA DA POPULAÇÃO. Depende das taxas de natalidade e mortalidade, da expectativa de vida das pessoas... Grande Dicionário Enciclopédico

Conceitos de análise matemática. Diz-se que uma função f(x) é crescente no segmento se, para qualquer par de pontos x1 e x2, a≤x1 ... dicionário enciclopédico

Conceitos de matemática. análise. A função f(x) é chamada. aumentando no segmento [a, b], se para qualquer par de pontos x1 e x2, e<или=х1 <х<или=b, выполняется неравенство f(x1)Ciência natural. dicionário enciclopédico

Ramo da matemática que estuda derivadas e diferenciais de funções e suas aplicações ao estudo de funções. Projeto de D. e. em uma disciplina matemática independente está associada aos nomes de I. Newton e G. Leibniz (segunda metade de 17 ... Grande Enciclopédia Soviética

Ramo da matemática em que se estudam os conceitos de derivada e diferencial e como eles são aplicados ao estudo de funções. Desenvolvimento de D. e. intimamente relacionado ao desenvolvimento do cálculo integral. Seu conteúdo também é inseparável. Juntos eles formam a base... ... Enciclopédia Matemática

Este termo tem outros significados, veja função. A solicitação "Display" é redirecionada aqui; veja também outros significados... Wikipedia

Aristóteles e os Peripatéticos- A Questão de Aristóteles Vida de Aristóteles Aristóteles nasceu em 384/383. AC e. em Estagira, na fronteira com a Macedónia. Seu pai, chamado Nicômaco, era médico a serviço do rei macedônio Amintas, pai de Filipe. Junto com sua família, o jovem Aristóteles... ... Filosofia ocidental desde suas origens até os dias atuais

- (QCD), teoria quântica de campos da forte interação de quarks e glúons, construída na imagem do quantum. eletrodinâmica (QED) baseada na simetria do medidor de “cor”. Ao contrário do QED, os férmions no QCD possuem propriedades complementares. grau quântico de liberdade número,… … Enciclopédia física

I Coração O coração (latim cor, grego cardia) é um órgão fibromuscular oco que, funcionando como bomba, garante a circulação do sangue no sistema circulatório. Anatomia O coração está localizado no mediastino anterior (Mediastino) no Pericárdio entre... ... Enciclopédia médica

A vida de uma planta, como qualquer outro organismo vivo, é um conjunto complexo de processos inter-relacionados; O mais significativo deles, como se sabe, é a troca de substâncias com o meio ambiente. O meio ambiente é a fonte de onde... ... Enciclopédia biológica