Normální formy: dnf, knf, sdnf, sknf. Speciální reprezentace booleovských funkcí Konjunktivní normální forma booleovské funkce se nazývá
Pro jakýkoli logický vzorec je možné pomocí identických transformací sestavit nekonečné množství jemu ekvivalentních vzorců. V algebře logiky je jedním z hlavních úkolů hledání kanonických forem (tj. vzorců sestavených podle jediného pravidla, kánonu).
Pokud je logická funkce vyjádřena pomocí disjunkce, konjunkce a negace proměnných, pak se tato forma zobrazení nazývá normální.
Mezi normálními formami vynikají dokonalé normální formy (ty formy, ve kterých jsou funkce zapsány jedinečným způsobem).
Dokonalá disjunktivní normální forma (PDNF)
Definice. Vzorec se nazývá elementární konjunkce, pokud je tvořen konjunkcí určitého počtu proměnných nebo jejich negací.
Příklady: y, ¬ y, x 1 ∧ ¬ x 2 ∧ x 3 ∧ x 4
Definice. Formule se nazývá disjunktivní normální forma (DNF), pokud se jedná o disjunkci neopakujících se elementárních spojek.
DNF se zapisuje v následujícím tvaru: F 1 ∨ F 2 ∨ ... ∨ F n , kde F i je elementární spojka
Příklady: ¬ x 1 ∧ x 2 ∨ x 1 ∧ ¬ x 2 ∨ x 1 ∧ ¬ x 2 ∧ x 3, ¬ y 1 ∨ y 1 ∧ y 2 ∨ ¬ y 2
Definice. Logický vzorec v k proměnných se nazývá dokonalá disjunktivní normální forma (PDNF), pokud:
1) vzorec je DNF, ve kterém každá elementární konjunkce je konjunkcí k proměnných x 1 , x 2 , ..., x k a na i-tém místě této konjunkce je buď proměnná x i, nebo její negace;
2) všechny elementární konjunkce v takovém DNF jsou párově odlišné.
Příklad: (¬ x 1 ∧ x 2 ∧ x 3) ∨ (x 1 ∧ ¬ x 2 ∧ x 3) ∨ (x 1 ∧ x 2 ∧ ¬ x 3)
Dokonalá konjunktivní normální forma (SKNF)
Definice. Formule se nazývá elementární disjunkce, pokud je tvořena disjunkcí určitého počtu proměnných nebo jejich negací.
Příklady: ¬ x 3, x 1 ∨ x 2, x 1 ∨ x 2 ∨ ¬ x 3
Definice. Vzorec se nazývá konjunktivní normální forma (CNF), pokud je konjunkcí neopakujících se elementárních disjunkcí.
CNF se zapisuje v následujícím tvaru: F 1 ∧ F 2 ∧ ... ∧ F n , kde F i je elementární disjunkce
Příklady: (x 1 ∨ ¬ x 2) ∧ x 3, (x 1 ∨ x 2) ∧ (¬ x 1 ∨ x 2 ∨ x 3) ∧ (x 1 ∨ ¬ x 2 ∨ ¬ x 3)
Definice. Logický vzorec v k proměnných se nazývá dokonalá konjunktivní normální forma (KDNF), pokud:
1) vzorec je CNF, ve kterém každá elementární disjunkce je disjunkcí k proměnných x 1 , x 2 , …, x k , a i-té místo této disjunkce je buď proměnná x i nebo její negace;
2) všechny elementární disjunkce v takovém CNF jsou párově odlišné.
Příklad: (x 1 ∨ x 2 ∨ x 3) ∧ (¬ x 1 ∨ ¬ x 2 ∨ x 3)
všimněte si, že jakákoli logická funkce, která není shodně rovna 0 nebo 1, může být reprezentována jako SDNF nebo SKNF.
Algoritmus pro konstrukci SDNF podle pravdivostní tabulky
- Vyberte všechny řádky tabulky, ve kterých je hodnota funkce rovna jedné.
- Pro každý takový řádek napište konjunkci všech proměnných následovně: pokud je hodnota některé proměnné v této množině rovna 1, pak do konjunkce zahrneme i samotnou proměnnou, v opačném případě její negaci.
- Všechny výsledné spojky spojujeme disjunkčními operacemi.
Algoritmus pro konstrukci SKNF podle pravdivostní tabulky
- Vyberte všechny řádky tabulky, ve kterých je hodnota funkce rovna nule.
- Pro každý takový řádek zapište disjunkci všech proměnných následovně: je-li hodnota některé proměnné v této množině 0, zahrneme do konjunkce samotnou proměnnou, v opačném případě její negaci.
- Všechny získané disjunkce spojujeme operacemi konjunkce.
Analýza algoritmů ukazuje, že pokud je hodnota funkce rovna 0 na většině řádků pravdivostní tabulky, pak pro získání jejího logického vzorce je lepší sestrojit SDNF, jinak - SKNF.
Příklad: Je dána pravdivostní tabulka logické funkce tří proměnných. Sestavte logický vzorec, který implementuje tuto funkci.
| X | y | z | F(x, y, z) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Protože na většině řádků pravdivostní tabulky je hodnota funkce rovna 1, pak sestrojíme SKNF. V důsledku toho dostaneme následující logický vzorec:
F = (¬x ∨ y ∨ z) ∧ (¬x ∨ y ∨ ¬z)
Zkontrolujeme výsledný vzorec. K tomu sestrojíme pravdivostní tabulku funkce.
| X | y | z | X | ¬ x ∨ y ∨ z | ¬z | ¬ x ∨ y ∨ ¬ z | F(x, y, z) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Při porovnání původní pravdivostní tabulky a tabulky vytvořené pro logický vzorec si všimneme, že sloupce funkčních hodnot jsou stejné. To znamená, že logická funkce je sestavena správně.
Disjunktivní a konjunktivní normální formy výrokové algebry. Pro každou funkci výrokové logiky lze sestavit pravdivostní tabulku. Inverzní problém je také vždy řešitelný. Uveďme několik definic.
Elementární konjunkce (konjunkce) se nazývají konjunkce proměnných nebo jejich negace, ve kterých se každá proměnná vyskytuje nejvýše
jednou.
Disjunktivní normální forma(DNF) je formule, která má tvar disjunkce elementárních spojek.
Elementární disjunkce (podle klauzulí) se nazývají disjunkce proměnných s negacemi nebo bez nich.
Konjunktivní normální forma(CNF) je formule, která má tvar konjunkce elementárních disjunkcí.
Pro každou funkci výrokové algebry lze najít sadu disjunktivních a konjunktivních normálních forem.
Algoritmus konstrukce DNF:
1. Přejděte na Booleovské operace pomocí ekvivalentních transformačních vzorců.
2. Přejděte na vzorce s těsnou negací, tedy na vzorec, ve kterém se negace nenacházejí výše než nad proměnnými – aplikujte de Morganovy zákony.
3. Otevřete závorky - použijte zákony distributivity.
4. Opakování pojmů na jeden čas - zákon idempotence.
5. Aplikujte zákony absorpce a semiabsorpce.
Příklad 6 Najděte vzorce DNF: .
V Booleově algebře, princip duality. Je to následovně.
Funkce je volána dvojí na funkci if . Tito. abychom našli funkci duální k dané, je nutné sestrojit negaci funkce z negací argumentů.
Příklad 7 Najděte funkci dual to .
Mezi základními funkcemi algebry logiky je 1 duální k 0 a naopak, x je duální k x, je duální k , je duální k a naopak.
Pokud ve vzorci F 1 představujícím funkci jsou nahrazeny všechny spojky
na disjunkci, disjunkci na konjunkci, 1 na 0, 0 na 1, pak dostaneme formuli F * , představující funkci * , duál .
Konjunktivní normální forma (CNF) je duální koncept pro DNF, takže ji lze snadno zkonstruovat podle schématu:
Příklad 8 Najděte vzorce CNF: .
S použitím výsledku příkladu 6 máme
Dokonalé disjunktivní a dokonalé konjunktivní normální formy. V každém z typů normálních forem (disjunktivní a konjunktivní) lze vyčlenit třídu dokonalých forem SDNF a SKNF.
Dokonalá elementární konjunkce je logickým součinem všech proměnných s negací nebo bez negace a každá proměnná je v součinu zahrnuta pouze jednou.
Libovolné DNF lze redukovat na SDNF rozdělením konjunkcí, které neobsahují všechny proměnné, tzn. sčítání pro chybějící proměnnou x i se násobí pomocí zákona distributivity
Příklad 9 Najděte SDNF pro příklad DNF 6
Dokonalá elementární disjunkce nazývá se logický součet všech proměnných s negacemi nebo bez nich, navíc každá proměnná je do součtu zahrnuta pouze jednou.
Jakýkoli CNF může být redukován na SKNF přidáním konjunkce, která neobsahuje žádnou proměnnou Xi konjunkcí a použitím distributivního zákona
Příklad 10. Převést CNF na SKNF:
Ke konstrukci SKNF můžete použít schéma
Příklad 11. Najděte SKNF pro vzorec z příkladu 6.
Každá funkce má SDNF a navíc jedinou . Každá funkce má SKNF a navíc jeden .
Protože SDNF a SKNF jsou jednoznačně definovány vzorci, lze je sestavit podle pravdivostní tabulky vzorce.
Pro konstrukci SDNF je nutné vybrat řádky, ve kterých F nabývá hodnotu 1 a zapsat k nim dokonalé elementární spojky. Pokud je hodnota proměnné v požadovaném řádku pravdivostní tabulky rovna jedné, pak se v dokonalé konjunkci bere bez negace, je-li nula, pak s negací. Poté jsou dokonalá konjunkce (jejich počet se rovná počtu jednotek v tabulce) spojena znaménky disjunkce.
Pro sestavení SKNF podle pravdivostní tabulky je nutné v ní vybrat řádky, kde F=0, a zapsat dokonalé elementární disjunkce a ty pak spojit znaménky konjunkce. Pokud v požadovaném řádku pravdivostní tabulky (F=0) hodnota proměnné odpovídá nule, pak se v dokonalé disjunkci bere bez negace, je-li rovna jedné, pak s negací.
Příklad 12. Najděte SDNF a SKNF podle pravdivostní tabulky pro vzorec z příkladu 6.
Tabulka 14 ukazuje pouze konečnou hodnotu F=10101101. Platnost tohoto tvrzení by měla být ověřena nezávisle vytvořením rozšířené pravdivostní tabulky.
Tabulka 14
| X | y | z | ||
Normální formy booleovských funkcí Reprezentace booleovské funkce ve formě disjunkce konjunktivních členů jednotkových konstituentů Ki 2.7 se nazývá disjunktivní normální forma DNF této funkce. obsahují přesně jednu po druhé všechny logické proměnné brané s negacemi nebo bez nich, pak se tato forma reprezentace funkce nazývá dokonalá disjunktivní normální forma SDNF této funkce. Jak vidíte, při kompilaci funkce SDNF musíte provést disjunkci všech mintermů, pro které má funkce hodnotu 1.
Sdílejte práci na sociálních sítích
Pokud vám tato práce nevyhovuje, dole na stránce je seznam podobných prací. Můžete také použít tlačítko vyhledávání
Přednáška 1.xx
Normální formy booleovských funkcí
Reprezentace booleovské funkce ve formě disjunkce konjunktivních členů (jednotkový prvek) K i
, (2.7)
volal disjunktivní normální forma(DNF) této funkce.
Pokud jsou všechny konjunktivní členy v DNF minterms , tj. obsahují přesně jednu po druhé všechny logické proměnné, brané s negacemi nebo bez nich, pak se tato forma reprezentace funkce nazýváperfektní disjunktivní normální forma(SDNF ) této funkce. SDNF se nazývá perfektní , protože každý člen v disjunkci zahrnuje všechny proměnné; disjunktivní , protože hlavní operací ve vzorci je disjunkce. Koncept "normální forma” znamená jednoznačný způsob zápisu vzorce, který implementuje danou funkci.
Vzhledem k výše uvedenému, věta 2.1 implikuje následující větu.
Věta 2. Jakákoli booleovská funkce(není identicky rovno 0) mohou být zastoupeny v SDNF, .
Příklad 3 Mějme tabulkovou funkci f (x 1, x 2, x 3) (tabulka 10).
Tabulka 10
|
f (x 1 , x 2 , x 3 ) |
|||
Na základě vzorce (2.6) získáme:
Jak vidíte, při kompilaci funkce SDNF musíte provést disjunkci všech mintermů, pro které má funkce hodnotu 1.
Reprezentace booleovské funkce ve formě konjunkce disjunktivních členů (složka nula) D i
, (2.8)
volal konjunktivní normální forma(CNF ) této funkce.
Pokud jsou všechny disjunktivní členy CNF maxterms , tj. obsahují přesně jednu po druhé všechny logické proměnné funkce, brané s negacemi nebo bez nich, pak se takový CNF nazývádokonalá konjunktivní normální forma(SKNF) této funkce.
Věta 3. Jakákoli booleovská funkce(není identicky rovno 1) lze předložit SKNF, a tato reprezentace je jedinečná.
Důkaz věty lze provést podobně jako důkaz věty 2.1 na základě následujícího Shannonova lemmatu o konjunktivním rozkladu.
Shannonovo lemma . Jakákoli booleovská funkce f (x 1 , x 2 , …, x m ) z m proměnné mohou být reprezentovány jako:
. (2.9)
Je třeba poznamenat, že obě formy reprezentace logické funkce (DNF a CNF) jsou teoreticky stejné ve svých schopnostech: jakýkoli logický vzorec může být reprezentován jak v DNF (kromě identické nuly), tak v CNF (kromě identické jednotky) . V závislosti na situaci může být znázornění funkce v té či oné formě kratší.
V praxi se nejčastěji používá DNF., protože tato forma je člověku známější: od dětství je zvyklý spíše sčítat produkty než násobit součty (v druhém případě chce intuitivně otevřít závorky a tím přejít na DNF).
Příklad 4. Pro funkci f (x 1, x 2, x 3 ), uvedené v tabulce. 10, napište to SKNF.
Na rozdíl od SDNF se při kompilaci SKNF v pravdivostní tabulce logické funkce musíte podívat na kombinace proměnných, pro které má funkce hodnotu 0, a vytvořit spojení odpovídajících maxtermů,ale proměnné je třeba brát s inverzní inverzí:
Je třeba poznamenat, že je nemožné přejít přímo z SDNF funkce do jejího SKNF nebo naopak. Při pokusu o takové transformace jsou získány funkce, které jsou inverzní k těm požadovaným. Výrazy pro funkce SDNF a SKNF lze přímo získat pouze z jejich pravdivostní tabulky.
Příklad 5. Pro funkci f (x 1, x 2, x 3 ), uvedené v tabulce. 10, zkuste přejít z SDNF na SKNF.
Pomocí výsledku příkladu 2.3 dostaneme:
Jak můžete vidět, pod obecnou inverzí dostáváme SKNF logické funkce, která je inverzní vzhledem k funkci získané v příkladu 2.4:
protože obsahuje všechny maxtermy, které nejsou ve výrazu pro SKNF uvažované funkce.
1. Pomocí vlastností operací (viz Tabulka 9) identity (), součtu modulo 2 (), implikace () přejdeme na operace AND, OR, NOT (na booleovskou bázi).
2. Pomocí vlastností negace a de Morganových zákonů (viz tabulka 9) dosáhneme toho, že operace negace se vztahují pouze na jednotlivé proměnné, nikoli na celé výrazy.
3. Pomocí vlastností logických operací AND a OR (viz tabulka 9) získáme normální tvar (DNF nebo CNF).
4. V případě potřeby přecházíme na dokonalé formy (SDNF nebo SKNF). Chcete-li například získat SKNF, často potřebujete použít vlastnost: .
Příklad 6 Převést na booleovskou funkci SKNF
Provedením kroků výše uvedeného algoritmu v pořadí dostaneme:
Pomocí absorpční vlastnosti získáme:
Tak jsme získali funkce CNF f (x 1, x 2, x 3 ). Abyste získali její SKNF, musíte každou disjunkci, ve které chybí jakákoli proměnná, zopakovat dvakrát s touto proměnnou a s její negací:
2.2.6. Minimalizace booleovských funkcí
Protože stejnou logickou funkci lze reprezentovat pomocí h osobní vzorce, pak nalezení nejjednoduššího pho R mule, která definuje booleovskou funkci, zjednodušuje logický obvod, který implementuje booleovskou funkci do tsyu. Minimální tvar lÓ logická funkcev nějakém základu můžeme uvažovat takový základ, který obsahuje minimální počet superpozic func Na základ, povolení a závorky. Je však obtížné postavit efektivní l algoritmus takové minimalizace se získáním minima v závorce fo r my.
Uvažujme jednodušší minimalizační problém při syntéze kombinačních obvodů, ve kterém se nehledá minimální hranatá forma funkce, ale její minimální DNF. Pro tento úkol existují jednoduché účinné algoritmy.
Quineova metoda
Funkce, která má být minimalizována, je reprezentována v SDNF a jsou na ni aplikovány všechny možné operace neúplného lepení
, (2.10)
a poté absorpce
, (2.11)
a tato dvojice kroků se aplikuje opakovaně. Je tedy možné redukovat řadu pojmů. Tento postup se opakuje, dokud nezůstane žádný termín, který lze spojit s jiným termínem.
Všimněte si, že levá strana rovnice (2.10) by mohla být okamžitě minimalizována jednodušším a zjevnějším způsobem:
Tato metoda je špatná, protože při takovéto přímé minimalizaci konjunktivní termíny buď zmizí, i když stále existují případy jejich použití pro lepení a absorbování se zbývajícími termíny.
Nutno podotknout, že Quineova metoda je poměrně časově náročná, takže pravděpodobnost, že se při transformacích dopustíte chyb, je poměrně vysoká. Jeho výhodou je ale to, že jej lze teoreticky použít pro libovolný počet argumentů a se zvyšujícím se počtem proměnných se transformace stávají méně komplikovanými.
Metoda Carnotovy mapy
Carnotova metoda map (tabulek) je názornější, časově méně náročný a spolehlivý způsob minimalizace logických funkcí, ale její použití je prakticky omezeno na funkce 3-4 proměnných, maximálně 5-6 proměnných.
Carnotova mapa toto je dvourozměrná tabulková forma reprezentace pravdivostní tabulky booleovské funkce, která usnadňuje nalezení minimálního DNF logických funkcí v grafické vizuální podobě. Každá buňka tabulky je spojena s mintermem SDNF minimalizované funkce, navíc tak, že libovolné osy symetrie tabulky odpovídají zónám, které jsou v nějaké proměnné vzájemně inverzní. Takové uspořádání buněk v tabulce umožňuje snadno určit přilepené členy SDNF (které se liší inverzním znaménkem pouze jedné proměnné): v tabulce jsou uspořádány symetricky.
Pravdivé tabulky a Karnaughovy mapy pro funkce AND a OR dvou jízdních pruhů E Proměnné jsou uvedeny na Obr. 8. V každé buňce mapy je zapsána hodnota. A hodnota funkce na množině hodnot argumentu odpovídající této buňce n tov.
A) A b) NEBO
Rýže. 8. Příklad Karnaughových map pro funkce dvou proměnných
V Karnaughově mapě je pro funkci And pouze jedna 1, takže ji nelze ničím slepit. Ve výrazu pro minimální funkci bude pouze termín odpovídající této 1:
f = x y.
V Karnaughově mapě jsou již tři jedničky pro funkci OR a lze vytvořit dva lepící páry, přičemž 1 odpovídá termínu xy , je použit dvakrát. Ve výrazu pro funkci minimum je potřeba napsat výrazy pro páry, které se mají slepit, ponechat v nich všechny proměnné, které se pro tento pár nemění, a odstranit proměnné, které mění jejich hodnotu. Pro horizontální lepení dostaneme X a pro vertikální y , ve výsledku dostaneme výraz
f = x + y.
Na Obr. 9 ukazuje pravdivostní tabulky dvou funkcí tří proměnných ( A ) a jejich Karnotovy mapy ( b a c). Funkce f 2 se od prvního liší tím, že není definován na třech sadách proměnných (v tabulce je to označeno pomlčkou).
Při určování minimální DNF funkce se používají následující pravidla. Všechny buňky obsahující 1 jsou spojeny do uzavřených obdélníkových oblastí tzv k-kostek , kde k = log 2 K , K číslo 1 v obdélníkové oblasti. V tomto případě by každá oblast měla být obdélník s počtem buněk 2 k , kde k = 0, 1, 2, 3, …. Pro k = nazývá se 1 obdélník jedna je krychle a obsahuje 2 1 = 2 jednotky; pro k = 2 obdélník obsahuje 2 2 = 4 jednotky a nazývá se dvoukrychlový; pro k = 3 plocha 2 3 = 8 jednotek volaných tříkrychlový ; atd. Lze volat jednotky, které nelze spojovat do obdélníků nulové kostky , které obsahují pouze jednu jednotku (2 0 = 1). Jak je vidět, pro dokonce k oblasti mohou být čtvercové (ale ne nutně), a pokud jsou liché k pouze obdélníky.
|
před naším letopočtem |
||||||
Rýže. 9. Příklad Karnaughových map pro funkce tří proměnných
Tyto oblasti se mohou překrývat, tj. stejné buňky mohou být zahrnuty v různých oblastech. Potom se minimální DNF funkce zapíše jako disjunkce všech odpovídajících konjunktivních členů k - kostky.
Každá z těchto oblastí na Karnaughově mapě je reprezentována v minimálním DNF konjunkcí, počtem argumentů, ve kterých je k menší než celkový počet argumentů funkce m , tedy toto číslo je m k . Každá konjunkce minimálního DNF je složena pouze z těch argumentů, které pro odpovídající oblast mapy mají hodnoty buď bez inverzí, nebo pouze s inverzemi, tedy nemění jejich hodnotu.
Při pokrytí mapových buněk uzavřenými oblastmi bychom se tedy měli snažit zajistit, aby počet oblastí byl minimální a každá oblast obsahovala co nejvíce buněk, protože v tomto případě bude počet výrazů v minimálním DNF minimální a počet argumentů v odpovídající konjunkci bude minimální.
Pro funkci podle Karnotovy mapy na Obr. 9, b najdeme
protože pro horní uzavřenou oblast proměnné x 1 a x 2 mají hodnoty bez inverzí, pro nižší x 1 záležitosti s inverzí a x 3 bez inverze.
Nedefinované hodnoty v mapě na obr. 9, PROTI lze předefinovat nahrazením nulou nebo jedničkou. Pro tuto funkci je zřejmé, že je výhodnější obě nejisté hodnoty nahradit 1. V tomto případě se vytvoří dvě oblasti, což jsou různé typy 2-krychlí. Pak výraz pro minimální funkci DNF bude následující:
Při konstrukci uzavřených oblastí je dovoleno sbalit Karnotovu mapu do válce jak horizontálně, tak vertikálně. R do svislých os se spojením protilehlých ploch ka R vy, tj. jednotky umístěné podél okrajů Carnotovy mapy symetricky h ale lze je i kombinovat.
Karnotovy mapy lze kreslit různými způsoby (obrázek 10).
|
x 2 x 3 |
||||||||||
a b
Rýže. 10. Různé způsoby zobrazení Carnotových map
pro funkci 3 proměnných
Ale nejpohodlnější verze Karnaughových map pro funkce 2-4 proměnných jsou ty, které jsou znázorněny na Obr. 11 tabulek, protože ukazují pro každou buňku A všechny proměnné jsou v přímé nebo inverzní formě.
a b
Rýže. jedenáct. Nejpohodlnější obrázek Carnotových map
pro funkce 3 ( a) a 4 (b) proměnné
Pro funkce 5 a 6 proměnných se použije metoda znázorněná na obr. 10, V .
Rýže. 12. Obrázek Karnaughovy mapy pro funkci 5 proměnných
Rýže. 13. Obrázek Karnaughovy mapy pro funkci 6 proměnných
Další související díla, která by vás mohla zajímat.vshm> |
|||
| 9020. | PRINCIP DUALITY. ROZŠÍŘENÍ BOOLEANSKÝCH FUNKCÍ V PROMĚNNÝCH. DOKONALÉ DISJUNKTIVNÍ A KONJUNKTIVNÍ NORMÁLNÍ FORMY | 96,34 kB | |
| Tato věta je konstruktivní, protože nám umožňuje sestavit pro každou funkci vzorec, který ji realizuje ve formě dokonalé d.s. F. K tomu v pravdivostní tabulce pro každou funkci označíme všechny řádky, ve kterých | |||
| 6490. | Popis a minimalizace logických funkcí | 187,21 kB | |
| Ve verbální formě je vyjádřen vztah mezi argumenty funkce a jejími hodnotami. Příklad: Funkce se třemi argumenty se vyhodnotí, když jsou libovolné dva nebo více argumentů funkce stejné. Spočívá v konstrukci pravdivostní tabulky obsahující hodnoty funkce pro všechny sady hodnot argumentů. V tomto příkladu podle pravdivostní tabulky dostaneme takový záznam ve tvaru DNF ... | |||
| 6707. | Návrh relačních databází. Konstrukční problémy v klasickém přístupu. Principy normalizace, normální formy | 70,48 kB | |
| Co je návrh relační databáze Je to sada vzájemně souvisejících vztahů, ve kterých jsou definovány všechny atributy, nastaveny primární klíče vztahu a nastaveny některé další vlastnosti vztahu, které se týkají principů zachování integrity. Proto musí být návrh databáze velmi přesný a ověřený. Ve skutečnosti je databázový projekt základem budoucího softwarového balíku, který bude používán dlouhou dobu a mnoha uživateli. | |||
| 4849. | Formy a způsoby realizace funkcí státu | 197,3 kB | |
| Pojem „funkce“ má v domácí a zahraniční vědecké literatuře odlišný význam. Ve filozofických a obecně sociologických termínech je považován za „vnější projev vlastností objektu v daném systému vztahů“; jako soubor běžných nebo specifických akcí jednotlivců nebo orgánů | |||
| 17873. | Formování logického UUD u žáků 3. ročníku | 846,71 kB | |
| Psychologické a pedagogické aspekty problému utváření logických univerzálních akcí u mladších školáků Metody hodnocení utváření logických UUD. Vypracování koncepce rozvoje všestranně vzdělávacích aktivit v systému všeobecného vzdělávání odpovídá novým společenským požadavkům. Nejdůležitějším úkolem moderního vzdělávacího systému je formování univerzálních vzdělávacích aktivit UUD. Utváření univerzálních vzdělávacích aktivit je klíčem k prevenci školních potíží. | |||
| 2638. | Technická implementace logických spojení v automatických blokovacích systémech | 1,04 MB | |
| Technická implementace logických spojení v automatických blokovacích systémech Technickou implementaci třímístného a čtyřmístného řídicího algoritmu AB lze dosáhnout pomocí reléového kontaktu a bezkontaktních diskrétních a integrálních logických prvků... | |||
| 10203. | UPLATNĚNÍ KONCEPCE RIZIKOVÉHO PŘÍSTUPU PRO KONSTRUKCI STRUKTUÁLNÍCH A LOGICKÝCH MODELŮ VZNIKU A VÝVOJE NOUZE | 70,8 kB | |
| Obecná analýza rizik Výrobní prostředí je nasyceno výkonnými technologickými systémy a technologiemi, které činí lidskou práci produktivní a méně fyzicky obtížnou, ale nebezpečnější. Riziko je charakterizováno neočekávaností a náhlostí nástupu nebezpečné situace. Každý den se potýkáme s řadou rizik, ale většina z nich zůstává potenciálních.Teorie rizik umožňuje kvantitativní posouzení negativního dopadu na člověka, ale i poškození jeho zdraví a života. | |||
| 11576. | Pojem, druhy a formy transakcí. Důsledky nedodržení požadované formy transakcí | 49,82 kB | |
| Rozpoznání transakce jako neplatných typů neplatných transakcí. Aplikovanou hodnotou práce v kurzu je zjednodušení konceptu transakce, tedy její veřejné prezentace v přístupnější podobě. | |||
| 6213. | Aproximace funkcí | 3,08 MB | |
| První spočívá v nahrazení některé funkce dané analyticky nebo tabulkově jinou funkcí blízkou té původní, ale jednodušší a pro výpočty pohodlnější. Například nahrazení funkce polynomem umožňuje získat jednoduché vzorce pro numerickou integraci a derivaci; nahrazení tabulky aproximační funkcí umožňuje získat hodnoty v jejích mezilehlých bodech. Vzniká také druhý problém obnovení funkce na určitém segmentu z hodnot funkce dané na tomto segmentu v diskrétní sadě bodů. Odpověď na takovou otázku... | |||
| 14058. | Vývoj funkcí státu | 29,99 kB | |
| Ruský stát jako právní fenomén musí především zajistit realizaci účelu státu a jeho základních ústavních charakteristik jako demokratického federálního právního sociálně sekulárního státu s republikánskou formou vlády. Hlavní účel státu je určen Čl. | |||
normální forma logická formule neobsahuje znaky implikace, ekvivalence a negace neelementárních vzorců.
Normální forma existuje ve dvou formách:
konjunktivní normální forma (CNF)-- spojení několika disjunkcí, například $\left(A\vee \overline(B)\vee C\right)\wedge \left(A\vee C\right)$;
disjunktivní normální forma (DNF)-- disjunkce několika spojek, například $\left(A\klín \overline(B)\klín C\vpravo)\vee \left(B\klín C\vpravo)$.
SKNF
Dokonalá konjunktivní normální forma (SKNF) je CNF, který splňuje tři podmínky:
neobsahuje shodné elementární disjunkce;
žádná z disjunkcí neobsahuje stejné proměnné;
každá elementární disjunkce obsahuje každou proměnnou v daném CNF.
Jakýkoli booleovský vzorec, který není identicky pravdivý, může být reprezentován v SKNF.
Pravidla pro konstrukci SKNF podle pravdivostní tabulky
Pro každou sadu proměnných, pro kterou funkce rovná se 0, zapíše se součet a proměnné, které mají hodnotu 1, se berou s negací.
SDNF
Dokonalá disjunktivní normální forma (PDNF) je DNF, který splňuje tři podmínky:
neobsahuje shodné elementární spojky;
žádná ze spojek neobsahuje stejné proměnné;
každá elementární konjunkce obsahuje každou proměnnou z daného DNF, navíc ve stejném pořadí.
Jakýkoli booleovský vzorec, který není identicky nepravdivý, může být v SDNF reprezentován navíc jedinečným způsobem.
Pravidla pro konstrukci SDNF podle pravdivostní tabulky
Pro každou sadu proměnných, ve které je funkce rovna 1, se zapíše součin a proměnné, které mají hodnotu 0, se berou s negací.
Příklady hledání SKNF a SDNF
Příklad 1
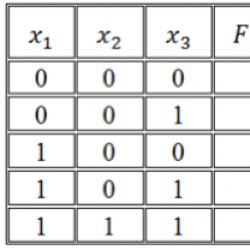
Napište logickou funkci podle její pravdivostní tabulky:
Obrázek 1.
Řešení:
Použijme pravidlo pro konstrukci SDNF:

Obrázek 2
Dostáváme SDNF:
Použijme stavební pravidlo SKNF.