Formas normais: dnf, knf, sdnf, sknf. Representações Especiais de Funções Booleanas A forma normal conjuntiva de uma função booleana é chamada
Para qualquer fórmula lógica, com a ajuda de transformações idênticas, é possível construir um número infinito de fórmulas equivalentes a ela. Na álgebra da lógica, uma das principais tarefas é a busca por formas canônicas (ou seja, fórmulas construídas de acordo com uma única regra, cânone).
Se uma função lógica é expressa por meio de disjunção, conjunção e negação de variáveis, então esta forma de representação é chamada de normal.
Dentre as formas normais, destacam-se as formas normais perfeitas (aquelas formas nas quais as funções são escritas de maneira única).
Forma Normal Disjuntiva Perfeita (PDNF)
Definição. Uma fórmula é chamada de conjunção elementar se for formada pela conjunção de um certo número de variáveis ou de suas negações.
Exemplos: y, ¬ y, x 1 ∧ ¬ x 2 ∧ x 3 ∧ x 4
Definição. Uma fórmula é chamada de forma normal disjuntiva (DNF) se for uma disjunção de conjunções elementares não repetidas.
DNF é escrito da seguinte forma: F 1 ∨ F 2 ∨ ... ∨ F n , onde F i é uma conjunção elementar
Exemplos: ¬ x 1 ∧ x 2 ∨ x 1 ∧ ¬ x 2 ∨ x 1 ∧ ¬ x 2 ∧ x 3, ¬ y 1 ∨ y 1 ∧ y 2 ∨ ¬ y 2
Definição. Uma fórmula lógica em k variáveis é chamada de forma normal disjuntiva perfeita (PDNF) se:
1) a fórmula é uma DNF, na qual cada conjunção elementar é uma conjunção de k variáveis x 1 , x 2 , ..., x k , e o i-ésimo lugar desta conjunção é a variável x i ou sua negação;
2) todas as conjunções elementares em tal DNF são distintas entre pares.
Exemplo: (¬ x 1 ∧ x 2 ∧ x 3) ∨ (x 1 ∧ ¬ x 2 ∧ x 3) ∨ (x 1 ∧ x 2 ∧ ¬ x 3)
Forma normal conjuntiva perfeita (SKNF)
Definição. Uma fórmula é chamada de disjunção elementar se for formada pela disjunção de um certo número de variáveis ou suas negações.
Exemplos: ¬ x 3, x 1 ∨ x 2, x 1 ∨ x 2 ∨ ¬ x 3
Definição. Uma fórmula é chamada de forma normal conjuntiva (CNF) se for uma conjunção de disjunções elementares não repetitivas.
CNF é escrito da seguinte forma: F 1 ∧ F 2 ∧ ... ∧ F n , onde F i é uma disjunção elementar
Exemplos: (x 1 ∨ ¬ x 2) ∧ x 3, (x 1 ∨ x 2) ∧ (¬ x 1 ∨ x 2 ∨ x 3) ∧ (x 1 ∨ ¬ x 2 ∨ ¬ x 3)
Definição. Uma fórmula lógica em k variáveis é chamada de forma normal conjuntiva perfeita (KDNF) se:
1) a fórmula é uma CNF, em que cada disjunção elementar é uma disjunção de k variáveis x 1 , x 2 , …, x k , e o i-ésimo lugar desta disjunção é a variável x i ou sua negação;
2) todas as disjunções elementares em tal CNF são distintas entre pares.
Exemplo: (x 1 ∨ x 2 ∨ x 3) ∧ (¬ x 1 ∨ ¬ x 2 ∨ x 3)
notar que qualquer função lógica que não seja identicamente igual a 0 ou 1 pode ser representada como SDNF ou SKNF.
Algoritmo para construção de SDNF de acordo com a tabela verdade
- Selecione todas as linhas da tabela em que o valor da função é igual a um.
- Para cada linha, escrevemos a conjunção de todas as variáveis da seguinte forma: se o valor de alguma variável neste conjunto for igual a 1, então incluímos a própria variável na conjunção, caso contrário, sua negação.
- Conectamos todas as conjunções resultantes por operações de disjunção.
Algoritmo para construção de SKNF de acordo com a tabela verdade
- Selecione todas as linhas da tabela em que o valor da função é igual a zero.
- Para cada linha, escrevemos a disjunção de todas as variáveis da seguinte forma: se o valor de alguma variável neste conjunto for 0, então incluímos a própria variável na conjunção, caso contrário, sua negação.
- Conectamos todas as disjunções obtidas por operações de conjunção.
A análise dos algoritmos mostra que se o valor da função for igual a 0 na maioria das linhas da tabela verdade, então para obter sua fórmula lógica é melhor construir um SDNF, caso contrário - SKNF.
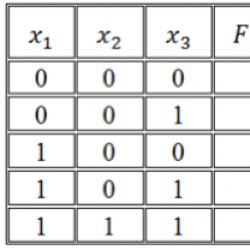
Exemplo: Dada uma tabela verdade de uma função lógica de três variáveis. Construa uma fórmula lógica que implemente esta função.
| x | sim | z | F(x, y, z) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Porque na maioria das linhas da tabela verdade, o valor da função é igual a 1, então construímos o SKNF. Como resultado, obtemos a seguinte fórmula lógica:
F = (¬x ∨ y ∨ z) ∧ (¬x ∨ y ∨ ¬z)
Vamos verificar a fórmula resultante. Para fazer isso, construímos uma tabela verdade da função.
| x | sim | z | x | ¬ x ∨ y ∨ z | ¬z | ¬ x ∨ y ∨ ¬ z | F(x, y, z) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Comparando a tabela verdade original e aquela construída para a fórmula lógica, notamos que as colunas de valores da função são as mesmas. Isso significa que a função lógica foi construída corretamente.
Formas normais disjuntivas e conjuntivas da álgebra proposicional. Para cada função da lógica proposicional, uma tabela verdade pode ser compilada. O problema inverso também é sempre solucionável. Vamos apresentar várias definições.
Conjunções elementares (conjuntos) são chamadas de conjunções de variáveis ou suas negações, nas quais cada variável ocorre no máximo
uma vez.
Forma normal disjuntiva(DNF) é uma fórmula que tem a forma de uma disjunção de conjunções elementares.
Disjunções elementares (por cláusulas) são chamadas disjunções de variáveis com ou sem negações.
Forma normal conjuntiva(CNF) é uma fórmula que tem a forma de uma conjunção de disjunções elementares.
Para cada função da álgebra proposicional, pode-se encontrar um conjunto de formas normais disjuntivas e conjuntivas.
Algoritmo de construção DNF:
1. Vá para operações booleanas usando fórmulas de transformação equivalentes.
2. Vá para fórmulas com negativos próximos, ou seja, para uma fórmula em que os negativos não estejam localizados acima das variáveis - aplique as leis de Morgan.
3. Abra os colchetes - aplique as leis da distributividade.
4. Repetir termos uma vez - a lei da idempotência.
5. Aplicar as leis da absorção e da semiabsorção.
Exemplo 6 Encontre fórmulas DNF: .
Na álgebra de Boole, princípio da dualidade. É o seguinte.
A função é chamada dual para a função se . Aqueles. para encontrar uma função dual a uma dada, é necessário construir a negação da função a partir das negações dos argumentos.
Exemplo 7 Encontre a função dual para.
Entre as funções elementares da álgebra da lógica 1 é dual para 0 e vice-versa, x é dual para x, é dual para, é dual para e vice-versa.
Se na fórmula F 1 que representa a função todas as conjunções forem substituídas
na disjunção, disjunção na conjunção, 1 em 0, 0 em 1, então obtemos a fórmula F * , representando a função * , dual .
A forma normal conjuntiva (CNF) é um conceito duplo para DNF, portanto pode ser facilmente construída de acordo com o esquema:
Exemplo 8 Encontre fórmulas CNF: .
Usando o resultado do Exemplo 6, temos
Formas normais disjuntivas perfeitas e conjuntivas perfeitas. Em cada um dos tipos de formas normais (disjuntivas e conjuntivas) pode-se destacar uma classe de formas perfeitas de SDNF e SKNF.
Uma conjunção elementar perfeita é um produto lógico de todas as variáveis com ou sem negação, e cada variável é incluída no produto apenas uma vez.
Qualquer DNF pode ser reduzido a SDNF dividindo conjunções que não contêm todas as variáveis, ou seja, adição para a variável ausente x i é multiplicada usando a lei da distributividade
Exemplo 9 Encontre SDNF para DNF exemplo 6
Disjunção elementar perfeitaé chamada a soma lógica de todas as variáveis com ou sem negações, além disso, cada variável é incluída na soma apenas uma vez.
Qualquer CNF pode ser reduzido a SKNF adicionando um termo de conjunção que não contenha nenhuma variável X i por conjunção e aplicando a lei distributiva
Exemplo 10. Converter CNF em SKNF:
Para construir o SKNF, você pode usar o esquema
Exemplo 11. Encontre SKNF para a fórmula do exemplo 6.
Toda função possui um SDNF e, além disso, o único. Cada função possui um SKNF e, além disso, um único arquivo .
Porque SDNF e SKNF são definidos exclusivamente por fórmulas e podem ser construídos de acordo com a tabela verdade da fórmula.
Para construir um SDNF, é necessário selecionar linhas nas quais F assume o valor 1 e escrever conjunções elementares perfeitas para elas. Se o valor da variável na linha desejada da tabela verdade for igual a um, então no conjunto perfeito ela é tomada sem negação, se for zero, então com negação. Então os conjuntos perfeitos (seu número é igual ao número de unidades na tabela) são conectados por sinais de disjunção.
Para construir o SKNF de acordo com a tabela verdade, é necessário selecionar linhas nela, onde F=0, e escrever disjunções elementares perfeitas, e então conectá-las com sinais de conjunção. Se na linha exigida da tabela verdade (F=0) o valor da variável corresponde a zero, então na disjunção perfeita ela é tomada sem negação, se for igual a um, então com negação.
Exemplo 12. Encontre SDNF e SKNF de acordo com a tabela verdade para a fórmula do exemplo 6.
A Tabela 14 mostra apenas o valor final F=10101101. A validade desta afirmação deve ser verificada de forma independente através da construção de uma tabela verdade expandida.
Tabela 14
| x | sim | z | ||
Formas normais de funções booleanas A representação de uma função booleana na forma de uma disjunção de termos conjuntivos de constituintes unitários Ki 2.7 é chamada de forma normal disjuntiva do DNF desta função. contém exatamente uma por uma todas as variáveis lógicas tomadas com ou sem negações, então esta forma de representação da função é chamada de forma normal disjuntiva perfeita do SDNF desta função. Como você pode ver, ao compilar uma função SDNF, é necessário fazer uma disjunção de todos os mintermos para os quais a função assume o valor 1.
Compartilhe o trabalho nas redes sociais
Se este trabalho não for do seu agrado, há uma lista de trabalhos semelhantes no final da página. Você também pode usar o botão de pesquisa
Aula 1.xx
Formas normais de funções booleanas
Representação de uma função booleana na forma de uma disjunção de termos conjuntivos (um constituinte unitário) K eu
, (2.7)
chamado forma normal disjuntiva(DNF) desta função.
Se todos os termos conjuntivos em DNF forem mintermos , ou seja, contém exatamente uma por uma todas as variáveis lógicas, tomadas com ou sem negações, então esta forma de representação da função é chamadaforma normal disjuntiva perfeita(SDNF ) desta função. SDNF é chamado perfeito , porque cada termo da disjunção inclui todas as variáveis; disjuntivo , porque a operação principal da fórmula é a disjunção. O conceito "forma normal”Significa uma maneira inequívoca de escrever uma fórmula que implementa uma determinada função.
Tendo em vista o acima exposto, o Teorema 2.1 implica o seguinte teorema.
Teorema 2. Qualquer função booleana(não é identicamente igual a 0) pode ser representado em SDNF, .
Exemplo 3 Deixe-nos ter uma função de tabela f (x 1, x 2, x 3) (Tabela 10).
Tabela 10
|
f (x 1 , x 2 , x 3 ) |
|||
Com base na fórmula (2.6), obtemos:
Como você pode ver, ao compilar uma função SDNF, é necessário fazer uma disjunção de todos os mintermos para os quais a função assume o valor 1.
Representação de uma função booleana na forma de uma conjunção de termos disjuntivos (constituinte zero) Eu
, (2.8)
chamado forma normal conjuntiva(CNF ) desta função.
Se todos os termos disjuntivos do CNF forem maxtermos , ou seja, contém exatamente uma por uma todas as variáveis lógicas da função, tomadas com ou sem negações, então tal CNF é chamadoforma normal conjuntiva perfeita(SKNF) desta função.
Teorema 3. Qualquer função booleana(não é identicamente igual a 1) pode ser submetido ao SKNF, e esta representação é única.
A prova do teorema pode ser realizada de forma semelhante à prova do Teorema 2.1 com base no seguinte lema de Shannon sobre decomposição conjuntiva.
Lema de Shannon . Qualquer função booleana f (x 1 , x 2 , …, x m ) de m variáveis podem ser representadas como:
. (2.9)
Deve-se notar que ambas as formas de representação de uma função lógica (DNF e CNF) são teoricamente iguais em suas capacidades: qualquer fórmula lógica pode ser representada tanto em DNF (exceto para o zero idêntico) quanto em CNF (exceto para a unidade idêntica) . Dependendo da situação, a representação da função de uma forma ou de outra pode ser mais curta.
Na prática, o DNF é o mais usado., porque esta forma é mais familiar para uma pessoa: desde criança ela está mais acostumada a somar produtos do que a multiplicar somas (neste último caso, ela intuitivamente quer abrir os colchetes e assim ir para DNF).
Exemplo 4. Para a função f (x 1, x 2, x 3 ), dado na Tabela. 10, escreva para SKNF.
Ao contrário do SDNF, ao compilar o SKNF, na tabela verdade de uma função lógica, você precisa observar as combinações de variáveis para as quais a função assume o valor 0 e fazer uma conjunção dos maxtermos correspondentes,mas as variáveis devem ser tomadas com inversão inversa:
Deve-se notar que é impossível passar diretamente do SDNF de uma função para o seu SKNF ou vice-versa. Ao tentar tais transformações, obtêm-se funções inversas às desejadas. Expressões para funções SDNF e SKNF podem ser obtidas diretamente apenas de sua tabela verdade.
Exemplo 5. Para a função f (x 1, x 2, x 3 ), dado na Tabela. 10, tente mudar de SDNF para SKNF.
Usando o resultado do exemplo 2.3 obtemos:
Como você pode ver, na inversão geral obtemos o SKNF de uma função lógica, que é inversa em relação à função obtida no exemplo 2.4:
uma vez que contém todos os maxtermos que não estão na expressão do SKNF da função em consideração.
1. Utilizando as propriedades das operações (ver Tabela 9) identidade (), soma módulo 2 (), implicação (), passamos para as operações AND, OR, NOT (para a base Boole).
2. Usando as propriedades de negação e as leis de Morgan (ver Tabela 9), conseguimos que as operações de negação se apliquem apenas a variáveis individuais, e não a expressões inteiras.
3. Utilizando as propriedades das operações lógicas AND e OR (ver Tabela 9), obtemos a forma normal (DNF ou CNF).
4. Se necessário, passamos para formas perfeitas (SDNF ou SKNF). Por exemplo, para obter o SKNF, muitas vezes é necessário usar a propriedade: .
Exemplo 6 Converter para função booleana SKNF
Executando as etapas do algoritmo acima em ordem, obtemos:
Usando a propriedade de absorção, obtemos:
Assim, obtivemos funções CNF f (x 1 , x 2 , x 3 ). Para obter seu SKNF, é necessário repetir cada disjunção, em que falta alguma variável, duas vezes com esta variável e com sua negação:
2.2.6. Minimização de funções booleanas
Como a mesma função lógica pode ser representada por h fórmulas pessoais e, em seguida, encontrar o Pho mais simples R mule que define uma função booleana simplifica o circuito lógico que implementa a função booleana para tsyu. Forma mínima lÓ função lógicaem alguma base, podemos considerar uma base que contém o número mínimo de superposições de funções Para base, permitindo e parênteses. Contudo, é difícil construir uma solução eficiente eu o algoritmo de tal minimização com obtenção do mínimo entre colchetes nós.
Considere um problema de minimização mais simples na síntese de circuitos combinacionais, no qual não se busca a forma mínima entre colchetes de uma função, mas seu DNF mínimo. Existem algoritmos simples e eficientes para esta tarefa.
Método Quine
A função a ser minimizada é representada em SDNF, e nela são aplicadas todas as operações possíveis de colagem incompleta
, (2.10)
e então absorção
, (2.11)
e este par de etapas é aplicado repetidamente. Assim, é possível reduzir a classificação dos termos. Este procedimento é repetido até que não reste nenhum termo que possa ser colado com qualquer outro termo.
Observe que o lado esquerdo da equação (2.10) poderia ser imediatamente minimizado de uma forma mais simples e óbvia:
Este método é ruim porque com essa minimização direta os termos conjuntivos ou desaparecem, embora ainda haja casos de seu uso para colagem e absorção com os demais termos.
Deve-se notar que o método de Quine é bastante demorado, portanto a probabilidade de cometer erros durante as transformações é bastante elevada. Mas a sua vantagem é que teoricamente pode ser utilizado para qualquer número de argumentos e, à medida que o número de variáveis aumenta, as transformações tornam-se menos complicadas.
Método do mapa de Carnot
O método de mapas (tabelas) de Carnot é uma forma mais visual, menos demorada e confiável de minimizar funções lógicas, mas seu uso é praticamente limitado a funções de 3-4 variáveis, máximo de 5-6 variáveis.
Mapa Carnot esta é uma forma tabular bidimensional de representação da tabela verdade de uma função booleana, o que facilita encontrar o DNF mínimo de funções lógicas em uma forma visual gráfica. Cada célula da tabela está associada ao mintermo do SDNF da função minimizada, aliás, de forma que quaisquer eixos de simetria da tabela correspondam a zonas que são mutuamente inversas em alguma variável. Tal disposição de células na tabela facilita a determinação dos termos SDNF aderidos (que diferem no sinal de inversão de apenas uma variável): eles são dispostos simetricamente na tabela.
Tabelas verdade e mapas de Karnaugh para funções AND e OR de duas pistas e As variáveis são apresentadas na fig. 8. Um valor é escrito em cada célula do mapa. A o valor da função no conjunto de valores do argumento correspondente a esta célula n tov.
A) E b) OU
Arroz. 8. Um exemplo de mapas de Karnaugh para funções de duas variáveis
Há apenas um 1 no mapa de Karnaugh para a função And, portanto não pode ser colado com nada. Na expressão para a função mínima, haverá apenas um termo correspondente a este 1:
f = x y .
Já existem três 1s no mapa de Karnaugh para a função OR, e dois pares de colagem podem ser feitos, sendo 1 correspondente ao termo xy , é usado duas vezes. Na expressão da função mínima, é necessário escrever os termos dos pares a serem colados, deixando neles todas as variáveis que não mudam para este par, e retirando as variáveis que mudam de valor. Para colagem horizontal, obtemos x , e para verticais sim , como resultado obtemos a expressão
f = x + y.
Na fig. 9 mostra as tabelas verdade de duas funções de três variáveis ( A ) e seus mapas de Karnot ( bec). Função f2 difere do primeiro porque não é definido em três conjuntos de variáveis (isso é indicado por um traço na tabela).
Ao determinar o DNF mínimo de uma função, são utilizadas as seguintes regras. Todas as células contendo 1 são combinadas em áreas retangulares fechadas chamadas k-cubos, onde k = log 2 K, K número 1 em uma área retangular. Neste caso, cada área deve ser um retângulo com o número de células 2 k , onde k = 0, 1, 2, 3,… . Para k = 1 retângulo é chamado um é um cubo e contém 2 1 = 2 unidades; para k = 2 retângulo contém 2 2 = 4 unidades e é chamado dois cubos; para k = 3 área de 2 3 = 8 unidades chamadas três cubos ; etc. Unidades que não podem ser combinadas em retângulos podem ser chamadas zero cubos , que contém apenas uma unidade (2 0 = 1). Como pode ser visto, mesmo para k as regiões podem ser quadradas (mas não necessariamente) e, se ímpares k apenas retângulos.
|
b c |
||||||
Arroz. 9. Um exemplo de mapas de Karnaugh para funções de três variáveis
Estas áreas podem se sobrepor, ou seja, as mesmas células podem ser incluídas em áreas diferentes. Então o DNF mínimo da função é escrito como uma disjunção de todos os termos conjuntivos correspondentes a k - cubos.
Cada uma dessas áreas no mapa de Karnaugh é representada no DNF mínimo por uma conjunção, cujo número de argumentos é k menor que o número total de argumentos da função eu , ou seja, este número é mk . Cada conjunção do DNF mínimo é composta apenas por aqueles argumentos que para a área correspondente do mapa possuem valores sem inversões ou apenas com inversões, ou seja, não alteram seu valor.
Assim, ao cobrir células do mapa com regiões fechadas, deve-se esforçar-se para garantir que o número de regiões seja mínimo, e que cada região contenha o maior número possível de células, pois neste caso o número de termos no DNF mínimo será mínimo e o o número de argumentos na conjunção correspondente será mínimo.
Para a função de acordo com o mapa de Karnot da Fig. 9, b encontramos
já que para a região fechada superior as variáveis x 1 e x 2 possuem valores sem inversões, para os inferiores x 1 importa com inversão, e x 3 sem inversão.
Valores indefinidos no mapa da fig. 9, V pode ser redefinido substituindo por zero ou um. Para esta função, fica claro que é mais vantajoso substituir ambos os valores incertos por 1. Nesse caso, formam-se duas regiões, que são tipos diferentes de 2 cubos. Então a expressão para a função DNF mínima será a seguinte:
Ao construir áreas fechadas, é permitido recolher o mapa de Karnot em um cilindro tanto horizontal quanto verticalmente. R aos eixos verticais com a união de faces opostas ka R você, ou seja, unidades localizadas ao longo das bordas do mapa de Carnot simetricamente h mas também pode ser combinado.
Os mapas de Karnot podem ser desenhados de diversas maneiras (Figura 10).
|
x 2 x 3 |
||||||||||
um b
Arroz. 10. Diferentes maneiras de representar mapas de Carnot
para uma função de 3 variáveis
Mas as versões mais convenientes dos mapas de Karnaugh para funções de 2 a 4 variáveis são aquelas mostradas na Fig. 11 tabelas, porque são mostradas para cada célula A todas as variáveis estão na forma direta ou inversa.
um b
Arroz. onze. A imagem mais conveniente dos mapas de Carnot
para funções 3 ( a) e 4 (b) variáveis
Para funções de 5 e 6 variáveis, o método mostrado na fig. 10, V.
Arroz. 12. Imagem de um mapa de Karnaugh para uma função de 5 variáveis
Arroz. 13. Imagem de um mapa de Karnaugh para uma função de 6 variáveis
Outros trabalhos relacionados que podem lhe interessar.vshm> |
|||
| 9020. | PRINCÍPIO DA DUALIDADE. EXPANSÃO DE FUNÇÕES BOOLEANAS EM VARIÁVEIS. FORMAS NORMAIS DISJUNTIVAS E CONJUNTIVAS PERFEITAS | 96,34 KB | |
| Este teorema é construtivo, pois nos permite construir para cada função uma fórmula realizando-a na forma de um d.s. f. Para fazer isso, na tabela verdade de cada função, marcamos todas as linhas em que | |||
| 6490. | Descrição e minimização de funções lógicas | 187,21 KB | |
| Na forma verbal, é expressa a relação entre os argumentos de uma função e seus valores. Exemplo: uma função de três argumentos é avaliada quando dois ou mais argumentos da função são iguais. Consiste na construção de uma tabela verdade contendo os valores da função para todos os conjuntos de valores dos argumentos. Neste exemplo, de acordo com a tabela verdade, obtemos tal entrada na forma de DNF... | |||
| 6707. | Projetando bancos de dados relacionais. Problemas de design na abordagem clássica. Princípios de normalização, formas normais | 70,48 KB | |
| O que é um design de banco de dados relacional?É um conjunto de relacionamentos inter-relacionados nos quais todos os atributos são definidos, as chaves primárias do relacionamento são definidas e algumas propriedades de relacionamento adicionais são definidas relacionadas aos princípios de manutenção da integridade. Portanto, o desenho do banco de dados deve ser muito preciso e verificado. Na verdade, o projeto de banco de dados é a base do futuro pacote de software que será utilizado por muito tempo e por muitos usuários. | |||
| 4849. | Formas e métodos de implementação das funções do Estado | 197,3 KB | |
| O termo “função” tem um significado diferente na literatura científica nacional e estrangeira. Em termos filosóficos e sociológicos gerais, é considerado como “uma manifestação externa das propriedades de um objeto num determinado sistema de relações”; como um conjunto de ações ordinárias ou específicas de indivíduos ou entidades | |||
| 17873. | Formação de UUD lógico em alunos do 3º ano | 846,71 KB | |
| Aspectos psicológicos e pedagógicos do problema da formação de ações lógicas universais em escolares mais jovens.Métodos de avaliação da formação de UUD lógico. O desenvolvimento de um conceito para o desenvolvimento de atividades educativas universais no sistema de ensino geral atende às novas demandas sociais. A tarefa mais importante do sistema educacional moderno é a formação de atividades educacionais universais UUD. A formação de atividades educativas universais é a chave para a prevenção das dificuldades escolares. | |||
| 2638. | Implementação técnica de conexões lógicas em sistemas de bloqueio automático | 1,04 MB | |
| Implementação técnica de conexões lógicas em sistemas de bloqueio automático A implementação técnica de algoritmos de controle AB de três e quatro dígitos pode ser alcançada usando contato de relé e elementos lógicos discretos e integrais sem contato... | |||
| 10203. | APLICAÇÃO DO CONCEITO DE ABORDAGEM ORIENTADA A RISCOS PARA CONSTRUÇÃO DE MODELOS ESTRUTURAIS E LÓGICOS DE ORIGEM E DESENVOLVIMENTO DE EMERGÊNCIAS | 70,8 KB | |
| Análise geral de riscos O ambiente de produção está saturado de poderosos sistemas tecnológicos e tecnologias que tornam o trabalho humano produtivo e menos difícil fisicamente, mas mais perigoso. O risco é caracterizado pelo inesperado e repentino início de uma situação perigosa. Todos os dias nos deparamos com inúmeros riscos, mas a maioria deles permanece potencial.A teoria do risco prevê uma avaliação quantitativa do impacto negativo sobre uma pessoa, bem como dos danos à sua saúde e à sua vida. | |||
| 11576. | O conceito, tipos e formas de transações. Consequências do não cumprimento da forma de transação exigida | 49,82 KB | |
| Reconhecimento da transação como tipos inválidos de transação inválida. O valor aplicado do trabalho da unidade curricular é simplificar o conceito de transação, ou seja, a sua apresentação pública de forma mais acessível. | |||
| 6213. | Aproximação de funções | 3,08 MB | |
| A primeira consiste em substituir alguma função dada analiticamente ou tabularmente por outra função próxima da original, porém mais simples e conveniente para cálculos. Por exemplo, substituir uma função por um polinômio permite obter fórmulas simples de integração e diferenciação numérica; substituir uma tabela por uma função de aproximação permite obter valores em seus pontos intermediários. Surge também o segundo problema de restaurar uma função em um determinado segmento a partir dos valores da função dados neste segmento em um conjunto discreto de pontos. A resposta para tal pergunta... | |||
| 14058. | A evolução das funções do estado | 29,99 KB | |
| O estado russo como fenômeno jurídico, em primeiro lugar, deve garantir a implementação do propósito do estado, bem como suas características constitucionais básicas como um estado social secular jurídico federal democrático com uma forma republicana de governo. A finalidade principal do Estado é determinada pelo art. | |||
forma normal a fórmula lógica não contém sinais de implicação, equivalência e negação de fórmulas não elementares.
A forma normal existe em duas formas:
forma normal conjuntiva (CNF)-- conjunção de diversas disjunções, por exemplo, $\left(A\vee \overline(B)\vee C\right)\wedge \left(A\vee C\right)$;
forma normal disjuntiva (DNF)-- disjunção de várias conjunções, por exemplo, $\left(A\wedge \overline(B)\wedge C\right)\vee \left(B\wedge C\right)$.
SKNF
Forma normal conjuntiva perfeita (SKNF) é um CNF que satisfaz três condições:
não contém disjunções elementares idênticas;
nenhuma das disjunções contém as mesmas variáveis;
cada disjunção elementar contém todas as variáveis no CNF fornecido.
Qualquer fórmula booleana que não seja identicamente verdadeira pode ser representada em SKNF.
Regras para construir SKNF de acordo com a tabela verdade
Para cada conjunto de variáveis para as quais função for igual a 0, a soma é escrita e as variáveis que possuem o valor 1 são tomadas com negação.
SDNF
Forma Normal Disjuntiva Perfeita (PDNF) é um DNF que satisfaz três condições:
não contém conjunções elementares idênticas;
nenhuma das conjunções contém as mesmas variáveis;
cada conjunção elementar contém todas as variáveis do DNF dado, além disso, na mesma ordem.
Qualquer fórmula booleana que não seja identicamente falsa pode ser representada em SDNF, além disso, de uma forma única.
Regras para construir SDNF de acordo com a tabela verdade
Para cada conjunto de variáveis em que a função é igual a 1, escreve-se o produto, e as variáveis que possuem valor 0 são tomadas com negação.
Exemplos de localização de SKNF e SDNF
Exemplo 1
Escreva uma função lógica de acordo com sua tabela verdade:
Imagem 1.
Solução:
Vamos usar a regra para construção do SDNF:

Figura 2.
Obtemos SDNF:
Vamos usar a regra de construção SKNF.